tikz绘制断开的曲线
Tikz 曲线的基本语法
1. 角度
如下命令
\draw[<->, gray] (0,0) to[relative, out=30, in=180-30] (0, 2);的含义是:绘制起点(0,0),终点(0,2),线段两段均绘制箭头,颜色为灰色,在起点处的切线角度相对于(0,0)和(0,2)的连线逆时针呈30°,终点处的切线与相对于连线呈150°的曲线方向相反。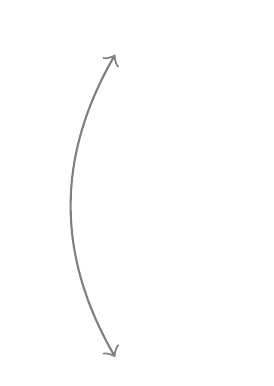
所谓“切线的角度”,选取的是沿着曲线方向为切线正方向。
由于(0,0)跟(0,2)之间连线的方向是90°,所以起点处的切线角度是90°+30°=120°,终点处跟90°+150°=240°相反,即240°-180°=60°。
上述命令就等价于
\draw[<->, gray] (0,0) to[out=120, in=240] (0, 2);2. 控制点
\draw[<->, gray] (0,0) to[relative, out=30, in=180-30] (0, 2);
\draw[<->, yellow] (1,0) to[out=120, in=240] (1, 2);
\draw[<->, green] (1,0) .. controls +(120:0.77994) and +(240:0.77994) .. (1,2);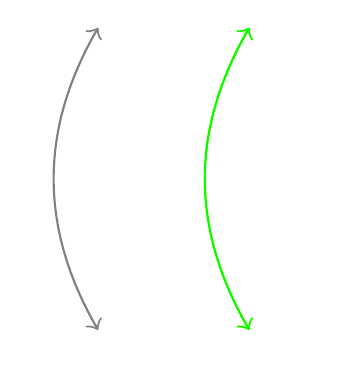
可以发现三条曲线形状一样,其中后两条几乎重合,放大之后有一点微小偏差,这是运算误差带来的,文末会分析此误差的来源。
对曲线
\draw[<->, green] (0,0) .. controls +(120:0.77994) and +(240:0.77994) .. (0,2);我们设起点为z0=(0,0),终点为z1=(0,2),两个控制点依次为c0, c1。
那么控制点的含义就是:向量c0-z0和z1-c1分别跟起点和终点处切线方向相同,控制点跟端点距离越远,曲线越向控制点的方向弯曲。
\draw[<->, magenta] (0,0) .. controls +(120:1) and +(240:1) .. (0,2);
\draw[<->, teal] (0,0) .. controls +(120:2) and +(240:2) .. (0,2);
代码中的+(120:1)分别表示+(240:1)相对于起点120°方向距离为1的点,和相对于终点240°方向距离为1的点,所以上一节中的in和out也可以统一解释为控制点相对于端点的方向。
理解了.. controls <first control point> and <second control point> ..语法的朋友,很自然可以想到上述代码还能等价地写成
\draw[<->] (0,0) to[controls=+(120:1) and +(240:1)] (0,2);或
\draw[<->] (0,0) .. controls ([shift=(120:1)]0,0) and ([shift=(240:1)]0,2) .. (0,2);3. looseness
一段(三次Bézier)曲线完全由两个端点和控制点决定,当仅给出in和out的参数时,tikz实际上用到了looseness参数的默认值。
looseness的值正比于控制点到端点的距离,默认是1。looseness越接近0,曲线相应的一端越接近直线;looseness的值越大,曲线相应的一端弯曲得越厉害。
三次 Bézier 曲线
起点为z0,终点为z1,前后控制点分别为c0, c1的三次Bézier曲线的方程为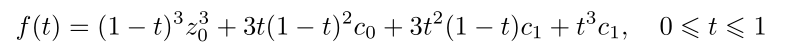
其中t是参数。
起点处的切线为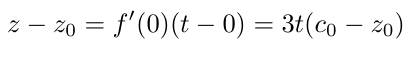 ,可见c0确实在这条切线上。
,可见c0确实在这条切线上。 时,
时,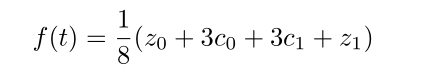
如果我们作三个一阶中点m0, m1和m2、两个二阶中点m3, m4以及三阶中点m5,m5即 时曲线上的点
时曲线上的点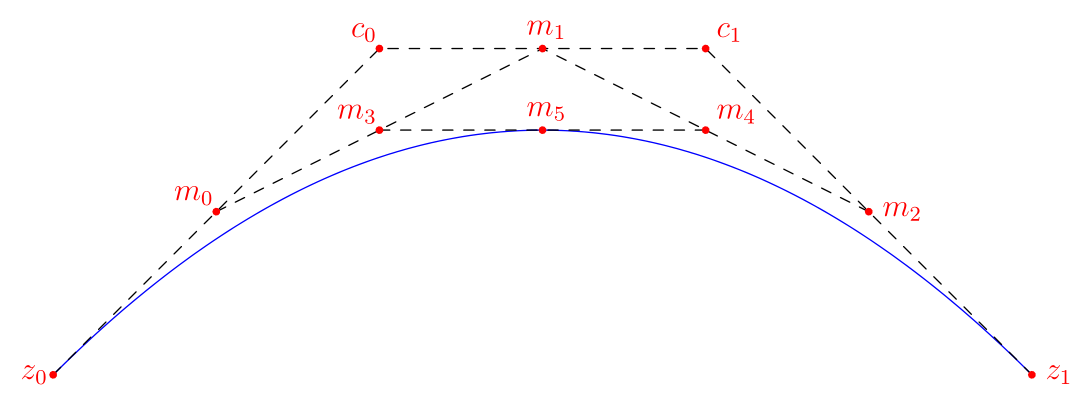
其中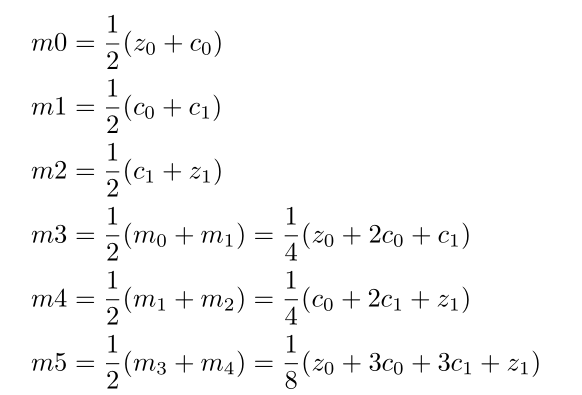
任何一点的导数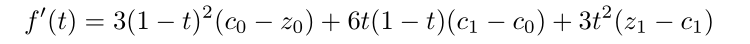
则有
有了以上数学工具之后,我们就可以画一个曲线的一部分。
比如f(t)的前一半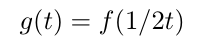
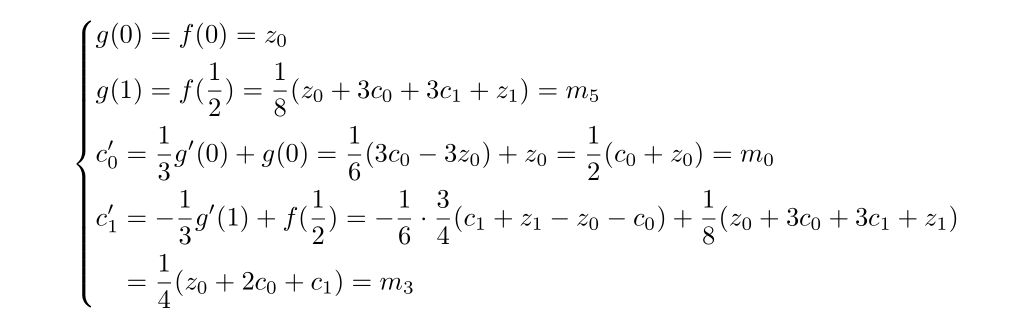
加载calc库后代码如下
\draw[<->, gray] (0,0) to[controls=+(120:1) and +(240:1)] (0,2);
\draw[<-, green] (0,0) .. controls +(120:0.5) and
($.25*(0,0)+.25*($(0,2)+(240:1)$)+.5*($(0,0)+(120:1)$)$) ..
($.125*(0,0)+.125*(0,2)+.375*($(0,0)+(120:1)$)+.375*($(0,2)+(240:1)$)$);有一个稍微简单一点的写法:
\draw[<->, gray] (0,0) to[controls=+(120:1) and +(240:1)] coordinate [midway](a) (0,2);
\draw[<-, green] (0,0) .. controls +(120:0.5) and
+($.125*(120:1)-.125*(240:1)-.25*(0,2)$) .. (a);
绘制中间断开的曲线
回到一开始的曲线
\draw[<->, gray] (0,0) to[relative, out=30, in=180-30] (0, 2);在tikz的实现中,控制点到端点的距离=looseness*0.38997*起点到终点的距离,就是1*0.38997*2=0.77994,前文中
\draw[<->, green] (0,0) .. controls +(120:0.77994) and +(240:0.77994) .. (0,2);就是这样得来。
一般地,从t=0到t=t0的一段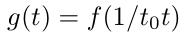
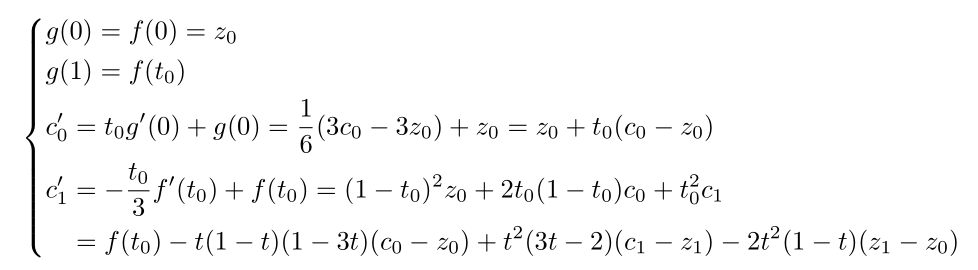
曲线的函数是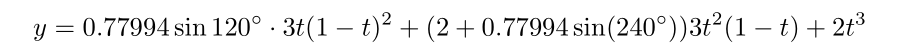
解出来f(t)=0.8和1.2时t的值为0.39936和0.60064,于是可以画
\path (0,0) to[relative, out=30, in=180-30] coordinate[pos=0.39936](a) coordinate[midway](c) coordinate[pos=0.60064](b) (0, 2);
\draw[<-, magenta] (0,0) .. controls +(120:0.39936*0.77994) and
(${2*0.39936*(1-0.39936)}*(120:.77994)+pow(0.39936,2)*($(0,2)+(240:.77994)$)$) .. (a);
\draw[->, magenta] (b) .. controls (${(1-0.39936)*(1+0.39936)}*(0,2)+{2*0.39936*(1-0.39936)}*(240:.77994)+pow(0.39936,2)*(120:.77994)$) and
+(240:0.39936*0.77994).. (0,2);
\node at (c) {Label};
最终实现
有一个简单但不太可靠的方法
\begin{tikzpicture}
\draw [gray] (0,0) to[relative, out=-30, in=-150](0,2);
\path[save path=\A](0,0) to[relative, out=30, in=150] coordinate[midway] (A) (0,2);
\begin{tikzpicture}[overlay]
\begin{pgfinterruptboundingbox}
\clip (A) +(-.5,-.2) -| +(.5,.2)-| +(-.5,-.2)--cycle
(current bounding box.north east) --
(current bounding box.south east) --
(current bounding box.south west) --
(current bounding box.north west) --
(current bounding box.north east);
\end{pgfinterruptboundingbox}
\draw[magenta, <->, use path=\A];
\end{tikzpicture}
\node[teal] at (A) {Label};
\end{tikzpicture}
\documentclass{article}
\usepackage{tikz, etoolbox}
\usetikzlibrary{calc, ntersections}
\makeatletter
\let\saved@tikz@to@curve@path=\tikz@to@curve@path
\tikzoption{labeled to}{%
\ifx\tikz@to@or@edge@function\tikz@do@to
\pgfutil@ifstrequal{#1}{off}{\let\tikz@to@curve@path=\saved@tikz@to@curve@path}
{\patchcmd{\tikz@to@curve@path}{\tikz@computed@path}{%
\pgfextra{\tikz@labeled@to@exec{#1}%
\let\tikz@to@curve@path=\saved@tikz@to@curve@path}%
\tikz@computed@path
}{}{}%
}%
\fi
}
\newif\iftikz@labeled@to@start@outside@of@placeholder
\newif\iftikz@labeled@to@placeholder@pgf
\def\solve@bezier#1#2#3{\pgfmathsetmacro#1{#3}\pgfmathsetmacro#2{1-#3}}
\def\tikz@labeled@to@cut@curve#1{%
\pgfintersectionsortbyfirstpath
\pgfintersectionofpaths
{
\pgfpathmoveto{\pgfpoint@tikz@labeled@to@from}%
\pgfpathcurveto{\pgfpoint@tikz@labeled@to@control@i}
{\pgfpoint@tikz@labeled@to@control@ii}
{\pgfpoint@tikz@labeled@to@to}%
}
{
\iftikz@labeled@to@placeholder@pgf
#1
\else
\path (labeled to/placeholder) #1 \pgfextra{\pgfgetpath{\relax=\relax\global\let\temppath}};
\pgfsetpath\temppath
}%
}
\def\tikz@labeled@to@savecurrentpoint#1{%
\edef#1{\noexpand\pgfqpoint{\the\numexpr\pgf@x sp}{\the\numexpr\pgf@y sp}}%
}
\def\tikz@labeled@to@parse@specs{%
\pgfutil@ifnextchar[{\tikz@labeled@to@parse@specs@}{\tikz@labeled@to@parse@specs@[]}%
}
\def\tikz@labeled@to@parse@specs@[#1]#2#3{%
\tikz@labeled@to@start@outside@of@placeholdertrue
\tikz@labeled@to@placeholder@pgffalse
\foreach \tikz@labeled@to@spec in {#1} {%
\pgfutil@ifstrequal{\tikz@labeled@to@spec}{revert}{\tikz@labeled@to@start@outside@of@placeholderfalse}{}%
\pgfutil@ifstrequal{\tikz@labeled@to@spec}{pgf}{\tikz@labeled@to@placeholder@pgftrue}{}%
}
\tikz@labeled@to@parse@anchor{#2}
\def\tikz@labeled@to@placeholder@code{#3}
}
\def\tikz@labeled@to@parse@first@token#1#2\@nil{\let\tikz@labeled@to@let@token=#1}
\def\tikz@labeled@to@parse@anchor#1{%
\tikz@labeled@to@parse@first@token#1\@nil
\expandafter\ifcat\noexpand\tikz@labeled@to@let@token+%
\if\tikz@labeled@to@let@token+%
\expandafter\pgfutil@firstoftwo
\else
\if\tikz@labeled@to@let@token(%
\expandafter\expandafter\expandafter\pgfutil@firstoftwo
\else % is number, treat as time
\expandafter\expandafter\expandafter\pgfutil@secondoftwo
\fi
\fi
{\tikz@scan@one@point\pgfutil@firstofone#1}
{\pgfpointcurveattime{#1}
{\pgfpoint@tikz@labeled@to@from}
{\pgfpoint@tikz@labeled@to@control@i}
{\pgfpoint@tikz@labeled@to@control@ii}
{\pgfpoint@tikz@labeled@to@to}%
}%
\else % start with a command (like \pgfpoint)
#1%
\fi
\pgfcoordinate{labeled to/placeholder}{\pgfqpoint{\pgf@x}{\pgf@y}}%
}
\def\tikz@labeled@to@compute@subpath#1#2#3#4#5#6{%
\pgfmathsetmacro{\tikz@labeled@to@temp@time@i}{#1}%
\pgfmathsetmacro{\tikz@labeled@to@temp@time@ii}{#2}%
#3\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@temp@begin
#4\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@temp@control@i
#5\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@temp@control@ii
#6\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@temp@end
%
\pgfmathparse{\tikz@labeled@to@temp@time@i==0}%
\ifodd\pgfmathresult
\pgfmathparse{\tikz@labeled@to@temp@time@ii==1}%
\ifodd\pgfmathresult
\let\pgfpoint@tikz@labeled@to@subpath@begin=\pgfpoint@tikz@labeled@to@temp@begin
\let\pgfpoint@tikz@labeled@to@subpath@control@i=\pgfpoint@tikz@labeled@to@temp@control@i
\let\pgfpoint@tikz@labeled@to@subpath@control@ii=\pgfpoint@tikz@labeled@to@temp@control@ii
\let\pgfpoint@tikz@labeled@to@subpath@end=\pgfpoint@tikz@labeled@to@temp@end
\else
\let\pgfpoint@tikz@labeled@to@subpath@begin=\pgfpoint@tikz@labeled@to@temp@begin
\pgfpointcurveattime{\tikz@labeled@to@temp@time@ii}
{\pgfpoint@tikz@labeled@to@temp@begin}
{\pgfpoint@tikz@labeled@to@temp@control@i}
{\pgfpoint@tikz@labeled@to@temp@control@ii}
{\pgfpoint@tikz@labeled@to@temp@end}%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@subpath@end
%
\pgfpointlineattime{\tikz@labeled@to@temp@time@ii}{\pgfpoint@tikz@labeled@to@temp@begin}{\pgfpoint@tikz@labeled@to@temp@control@i}%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@subpath@control@i
% quadratic bezier curve is also cubic
\pgfpointcurveattime{\tikz@labeled@to@temp@time@ii}{\pgfpoint@tikz@labeled@to@temp@begin}
{\pgfpointlineattime{2/3}{\pgfpoint@tikz@labeled@to@temp@begin}{\pgfpoint@tikz@labeled@to@temp@control@i}}
{\pgfpointlineattime{2/3}{\pgfpoint@tikz@labeled@to@temp@control@ii}{\pgfpoint@tikz@labeled@to@temp@control@i}}
{\pgfpoint@tikz@labeled@to@temp@control@ii}%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@subpath@control@ii
\fi
\else
\pgfmathparse{\tikz@labeled@to@temp@time@ii==1}%
\ifodd\pgfmathresult
\let\pgfpoint@tikz@labeled@to@subpath@end=\pgfpoint@tikz@labeled@to@temp@end
\pgfpointcurveattime{\tikz@labeled@to@temp@time@i}
{\pgfpoint@tikz@labeled@to@temp@begin}
{\pgfpoint@tikz@labeled@to@temp@control@i}
{\pgfpoint@tikz@labeled@to@temp@control@ii}
{\pgfpoint@tikz@labeled@to@temp@end}%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@subpath@begin
%
\pgfpointlineattime{1-\tikz@labeled@to@temp@time@i}{\pgfpoint@tikz@labeled@to@temp@end}{\pgfpoint@tikz@labeled@to@temp@control@ii}%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@subpath@control@ii
%
\pgfpointcurveattime{1-\tikz@labeled@to@temp@time@i}{\pgfpoint@tikz@labeled@to@temp@end}
{\pgfpointlineattime{2/3}{\pgfpoint@tikz@labeled@to@temp@end}{\pgfpoint@tikz@labeled@to@temp@control@ii}}
{\pgfpointlineattime{2/3}{\pgfpoint@tikz@labeled@to@temp@control@i}{\pgfpoint@tikz@labeled@to@temp@control@ii}}
{\pgfpoint@tikz@labeled@to@temp@control@i}%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@subpath@control@i
\else
\tikz@labeled@to@compute@subpath{\tikz@labeled@to@temp@time@i}{1}{#3}{#4}{#5}{#6}%
\tikz@labeled@to@compute@subpath{0}{\tikz@labeled@to@temp@time@ii}
{\pgfpoint@tikz@labeled@to@subpath@begin}
{\pgfpoint@tikz@labeled@to@subpath@control@i}
{\pgfpoint@tikz@labeled@to@subpath@control@ii}
{\pgfpoint@tikz@labeled@to@subpath@end}%
\fi
\fi
}
\def\tikz@labeled@to@loop@body{%
\ifnum \i=1 %
\def\tikz@labeled@to@time@i{0}%
\pgfintersectiongetsolutiontimes{\i}{\tikz@labeled@to@time@ii}{\temp}%
\else
\pgfintersectiongetsolutiontimes{\the\numexpr\i-1\relax}{\tikz@labeled@to@time@i}{\temp}%
\ifnum\i>\pgfintersectionsolutions
\def\tikz@labeled@to@time@ii{1}%
\else
\pgfintersectiongetsolutiontimes{\i}{\tikz@labeled@to@time@ii}{\temp}%
\fi
\fi % if \i=1
\tikz@labeled@to@compute@subpath{\tikz@labeled@to@time@i}{\tikz@labeled@to@time@ii}
{\pgfpoint@tikz@labeled@to@from}
{\pgfpoint@tikz@labeled@to@control@i}
{\pgfpoint@tikz@labeled@to@control@ii}
{\pgfpoint@tikz@labeled@to@to}%
%
\pgfpoint@tikz@labeled@to@subpath@begin
\edef\tikzpoint@tikz@labeled@to@subpath@begin{(\the\pgf@x,\the\pgf@y)}%
\pgfpoint@tikz@labeled@to@subpath@control@i
\edef\tikzpoint@tikz@labeled@to@subpath@control@i{(\the\pgf@x,\the\pgf@y)}%
\pgfpoint@tikz@labeled@to@subpath@control@ii
\edef\tikzpoint@tikz@labeled@to@subpath@control@ii{(\the\pgf@x,\the\pgf@y)}%
\pgfpoint@tikz@labeled@to@subpath@end
\edef\tikzpoint@tikz@labeled@to@subpath@end{(\the\pgf@x,\the\pgf@y)}%
\edef\temp{%
\noexpand\draw \tikzpoint@tikz@labeled@to@subpath@begin
.. controls \tikzpoint@tikz@labeled@to@subpath@control@i and \tikzpoint@tikz@labeled@to@subpath@control@ii ..
\tikzpoint@tikz@labeled@to@subpath@end;%
\temp
}%
}
\def\tikz@labeled@to@exec#1{%
\pgfinterruptpath
\tikz@scan@one@point\pgfutil@firstofone(\tikztostart)%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@from
%
\tikz@scan@one@point\pgfutil@firstofone(\tikztotarget)%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@to
%
\tikz@scan@one@point\pgfutil@firstofone\tikz@computed@start%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@control@i
%
\tikz@scan@one@point\pgfutil@firstofone\tikz@computed@end%
\tikz@labeled@to@savecurrentpoint\pgfpoint@tikz@labeled@to@control@ii
%
\tikz@labeled@to@parse@specs#1%
\tikz@labeled@to@cut@curve{\tikz@labeled@to@placeholder@code}%
\def\tikz@labeled@to@path{}%
\foreach \i in {1,...,\numexpr\pgfintersectionsolutions+1\relax}
{
\iftikz@labeled@to@start@outside@of@placeholder
\ifodd\i
\tikz@labeled@to@loop@body
\fi
\else
\ifodd\i\else
\tikz@labeled@to@loop@body
\fi
\fi
}
\endpgfinterruptpath
}
\begin{document}
\begin{tikzpicture}
\path (0,0) to[relative, labeled to={{0.5}{+(-.5,-.2) rectangle +(.5,.2)}}, out=30, in=150] node{x} (0,2);
\end{tikzpicture}
\end{document}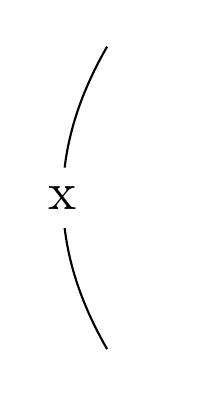
用法:labeled to={[<选项>]{<位置>}{<占位图形>}]
作用是以位置参数为参考点{0.5}{+(-.5,-.2) rectangle +(.5,.2)}的意思就是假设A是在曲线上t为0.5的点,将曲线在路径\path (A) +(-.5,-.2) rectangle +(.5,.2);内的部分断开。
位置参数可以写成tikz的坐标(如(0,1)、+(1,1)、(B)),或者pgf的点如\pgfqpointxy{1}{2},也可以写成一个数,表示曲线的时间参数。该点可用(labeled to/placeholder)引用。
如果占位图形的用pgf语法写成,需使用pgf选项。
默认曲线的起始位置在占位图形外部,否则需用revert选项。





