30 请问这种随机散点图用 Tikz 怎么画
发布于 2024-07-05 08:23:27
高中数学统计部分有时候会出这样的图, 带点随机性质, 然后又不是完全随机的, 如下图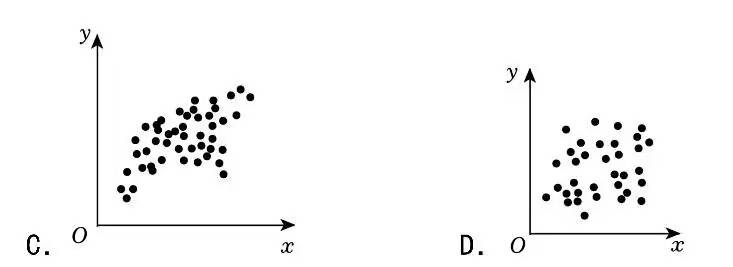
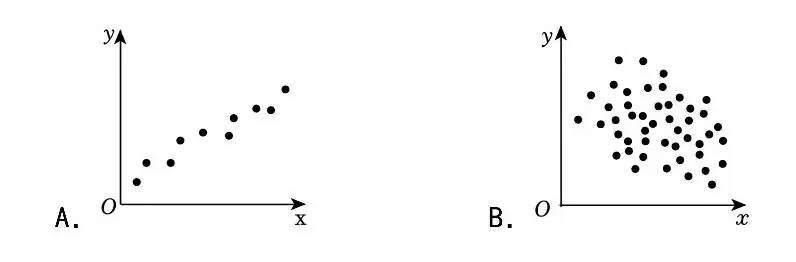
其中点最少的那个, 我模仿到一个代码如下
\begin{tikzpicture}
\tkzDefPoints{0/0/O,3.5/0/X,0/3.5/Y}
\draw[-stealth](O)--(X)node[below]{x};
\draw[-stealth](O)--(Y)node[right]{y};
\foreach \i in {1,2,...,10}
{
\coordinate (T) at ({0.3*\i},{0.3*\i+0.2*rand});
\tkzDrawPoints(T)
}
\tkzLabelPoints[below left](O)
\end{tikzpicture}但是对于比较复杂的其他选项, 就不知道怎么画了, 因此请教一下大佬们。谢谢。
关注者
0
被浏览
1.8k






感谢回答, 勉强看明白代码了. 还有一些问题请教. fpstepfromto 大约是均匀分布吗? 电脑中的大多数随机数是不是都是均匀分布? 比如那个 rand, 那么常见的正态分布随机数应该如何产生呢? 有这样的函数吗? 歇息.
@u13203
\fpstepfromto和\foreach\i in {1,2,...,n}类似,\fpstepfromto{0.5}{3}{10}会生成 10 个数字,a1=0.5,a10=3,相邻数字的差相等。TikZ 和
\fpeval的rand生成的数字都服从均匀分布。可以用
\tex_normaldeviate:D生成均值为 0,标准差为 65536 的服从正态分布的随机数。见更新的回答。
@u10307 非常感谢