公式太长,不知道如何折行
发布于 2021-04-05 07:38:15
这里有一个极其长的LaTeX写的公式 不知道怎么折行
\begin{equation}
2^{-M/2} \sum _{K=0}^M \sqrt{\binom{M}{K}} e^{i \gamma (K p-K q+m-n)+i K \left(\phi +\frac{\pi }{2}\right)} \text{Sum}\left[\frac{\left(\frac{z^2}{\pi ^2}+1\right)^{-\frac{| \mu | }{2}-\frac{1}{2}} \left(x^2+y^2\right)^{\frac{| \mu | }{2}} i^{-2 K q-2 n-| \mu | +\mu } \sqrt{\frac{2^{| \mu | +1} \left(\frac{1}{2} (K p+K q+m+n-|
\mu | )\right)!}{\left(\frac{1}{2} (K p+K q+m+n+| \mu | )\right)!}} \mathit{d}_{\frac{\mu }{2},\frac{1}{2} (K p-K q+m-n)}^{\frac{1}{2} (K p+K q+m+n)}(\beta ) L_{\frac{1}{2} (K p+K q+m+n-| \mu | )}^{\mu }\left(\frac{2 \left(x^2+y^2\right)}{\frac{z^2}{\pi ^2}+1}\right) \exp \left(2 i \pi \tilde{z}(x,y,z)-\frac{i \alpha \mu
}{2}+i \mu \arg (x+i y)+\frac{1}{2} i \alpha (K (p-q)+m-n)-i \tan ^{-1}\left(\frac{z}{\pi }\right) (K p+K q+m+n+1)-\frac{x^2+y^2}{\frac{z^2}{\pi ^2}+1}\right)}{\sqrt{\pi }},\{\mu ,-K p-K q-m-n,K p+K q+m+n,2\}\right]
\end{equation}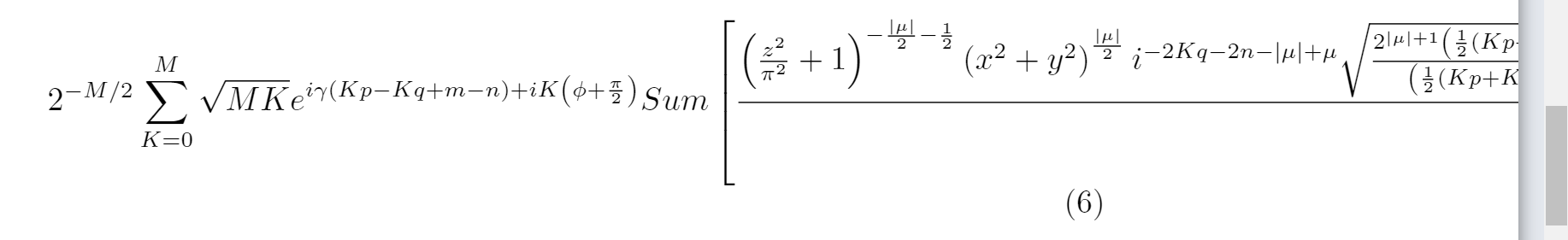
关注者
0
被浏览
2.3k

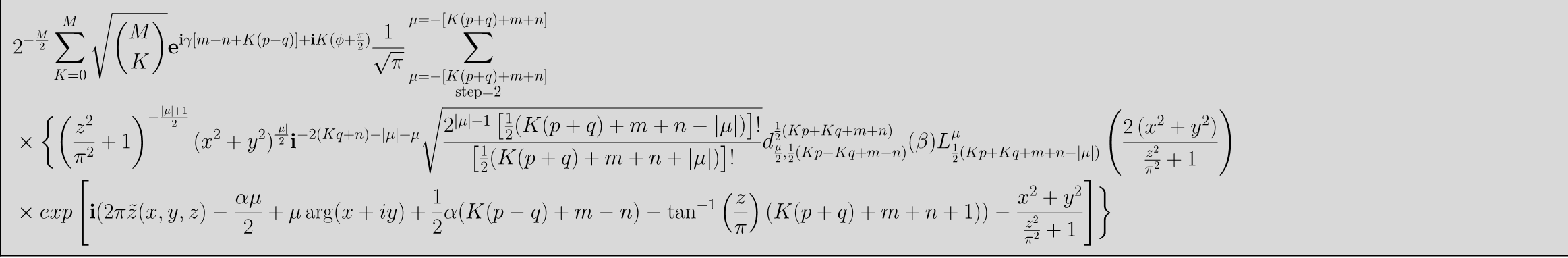






好的 谢谢