更新:
我 fork 了一份,增加了简单的解析功能,https://github.com/Sophanatprime/Polynomial-division 。
\PolySet{a}{1,-12,0,-42}
\PolySet{b}{1,-3}
$ \PolyLongDiv{a}{b} $
\quad
\PolySet{a}{1,-4,6,-4}
\PolySet{b}{1,-2}
$ \PolyLongDiv{a}{b} $
\PolySet*{a}{x^3-12x^2-42}
\PolySet*{b}{x-3}
$ \PolyLongDiv{a}{b} $\quad
$ \PolyLongDiv*[stage=4]{x^3-12x^2-42}{x-3} $
$ \PolyLongDiv*{-4x^2+x^3+6x-4x^0}{-2+x} $\quad
$ \PolyLongDiv*[var=y]{y^3-3y^2+3y-1}{y-1} $
$ \PolyPrint*{-4x^2+x^3+6x-4x^0} $
\PolySet{p}{1,0,1,1}
\PolySet{q}{2,1}
\PolySet{r}{1,0,1,0}
$ \PolyLongDiv[base=3]{r}{q} \quad \PolyLongDiv[base=3]{p}{q} $在 https://github.com/loopspace/Polynomial-division 的基础上,判断最高次系数是否为负,而不是将 \l__poly_uline_tl 直接修改: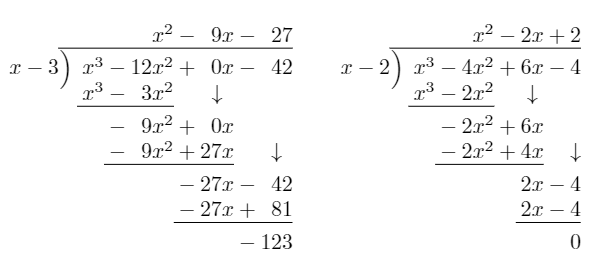
\documentclass{article}
%\url{http://tex.stackexchange.com/q/79411/86}
%\RequirePackage{xparse,expl3}
\ExplSyntaxOn
\bool_new:N \l__poly_zeros_bool
\bool_new:N \l__poly_first_bool
\bool_new:N \l__poly_trailing_bool
\bool_new:N \l__poly_ptrailing_bool
\bool_new:N \l__poly_stage_bool
\bool_new:N \l__poly_mod_bool
\bool_set_true:N \l__poly_stage_bool
\tl_new:N \l__poly_var_tl
\tl_new:N \l__poly_sep_tl
\tl_new:N \l__poly_longdiv_sep_tl
\tl_new:N \l__poly_oline_tl
\tl_new:N \l__poly_uline_tl
\tl_new:N \l__poly_neguline_tl
\tl_set:Nn \l__poly_var_tl {x}
\tl_set:Nn \l__poly_sep_tl {}
\tl_set:Nn \l__poly_longdiv_sep_tl {}
\int_new:N \l__poly_deg_int
\int_new:N \l__poly_pad_int
\int_new:N \l__poly_base_int
\int_new:N \l__poly_tmpa_int
\int_new:N \l__poly_tmpb_int
\int_new:N \l__poly_mod_tmpa_int
\int_new:N \l__poly_mod_tmpb_int
\int_new:N \l__poly_mod_tmpc_int
\int_new:N \l__poly_mod_tmpd_int
\int_new:N \l__poly_trailing_int
\int_new:N \l__poly_stage_int
\int_new:N \l__poly_cstage_int
\int_set:Nn \l__poly_pad_int{3}
\seq_new:N \l__poly_gtmpa_seq
\seq_new:N \l__poly_mod_seq
\keys_define:nn { polynomial }
{
stage .code:n = {
\bool_set_false:N \l__poly_stage_bool
\int_set:Nn \l__poly_stage_int {#1}
},
base .code:n = {
\bool_set_true:N \l__poly_mod_bool
\int_set:Nn \l__poly_base_int {#1}
\cs_set_eq:NN \poly_int_div:Nnn \poly_mod_int_div:Nnn
},
zeros .bool_set:N = \l__poly_zeros_bool,
separator .tl_set:N = \l__poly_sep_tl,
variable .tl_set:N = \l__poly_var_tl,
var .tl_set:N = \l__poly_var_tl,
% trailing .bool_set:N = \l__poly_trailing_bool
}
\cs_new_nopar:Npn \poly_print:N #1 {
\int_gset:Nn \l__poly_deg_int {\seq_count:N #1}
\int_gdecr:N \l__poly_deg_int
\int_gset:Nn \l__poly_tmpa_int {\l__poly_deg_int -
\l__poly_trailing_int+1}
\bool_gset_eq:NN \l__poly_ptrailing_bool \l__poly_trailing_bool
\bool_gset_true:N \l__poly_first_bool
\int_compare:nT {\l__poly_deg_int < \l__poly_pad_int} {
\prg_replicate:nn {2*(\l__poly_pad_int -
\l__poly_deg_int)}{\tl_use:N \l__poly_sep_tl}
}
\seq_map_inline:Nn #1 {
\bool_if:nTF {\int_compare_p:n {##1 == 0} && \l__poly_first_bool}
{
\tl_use:N \l__poly_sep_tl
\int_compare:nT {\l__poly_deg_int == 0}{0}
\tl_use:N \l__poly_sep_tl
}
{
\bool_if:nTF {\int_compare_p:n {##1 != 0} || \l__poly_zeros_bool}
{
\int_compare:nTF {##1 < 0}
{
\bool_if:NF \l__poly_first_bool {
\tl_use:N \l__poly_sep_tl
}
- \tl_use:N \l__poly_sep_tl
\bool_if:nF {\int_compare_p:n {##1 == -1} && \int_compare_p:n {\l__poly_deg_int > 0}}
{
\int_eval:n {-##1}
}
}
{
\bool_if:NF \l__poly_first_bool {\tl_use:N \l__poly_sep_tl+} \tl_use:N \l__poly_sep_tl
\bool_if:nF {\int_compare_p:n {##1 == 1} && \int_compare_p:n {\l__poly_deg_int > 0}}
{
##1
}
}
\int_compare:nT {\l__poly_deg_int > 0}
{
\tl_use:N \l__poly_var_tl
\int_compare:nT {\l__poly_deg_int > 1} {^{\int_use:N \l__poly_deg_int}}
}
}
{
\tl_use:N \l__poly_sep_tl
\tl_use:N \l__poly_sep_tl
}
\bool_gset_false:N \l__poly_first_bool
}
\int_gdecr:N \l__poly_deg_int
\bool_if:nT {\l__poly_ptrailing_bool && \int_compare_p:n {\l__poly_deg_int < \l__poly_tmpa_int}} {
\seq_map_break:
}
}
}
\cs_generate_variant:Nn \poly_print:N {c}
\cs_new_nopar:Npn \poly_reduce_mod:N #1 {
\bool_if:NT \l__poly_mod_bool
{
\seq_clear_new:N \l__poly_mod_seq
\int_step_inline:nnnn {1} {1} {\seq_count:N #1} {
\seq_put_left:Nx \l__poly_mod_seq {\int_mod:nn {\int_mod:nn {\seq_item:Nn #1 { - ##1}+0} {\l__poly_base_int} + \l__poly_base_int}{\l__poly_base_int}}
}
\seq_set_eq:NN #1 \l__poly_mod_seq
}
}
\cs_new_nopar:Npn \poly_add:NNN #1#2#3 {
\seq_clear_new:N #1
\int_step_inline:nnnn {1} {1} {\int_max:nn {\seq_count:N #2} {\seq_count:N #3}} {
\seq_put_left:Nx #1 {\int_eval:n {\seq_item:Nn #2 { - ##1} + \seq_item:Nn #3 { - ##1}+0}}
}
\poly_reduce_mod:N #1
}
\cs_generate_variant:Nn \poly_add:NNN {Ncc,ccc}
\cs_new_nopar:Npn \poly_sub:NNN #1#2#3 {
\seq_clear_new:N #1
\int_step_inline:nnnn {1} {1} {\int_max:nn {\seq_count:N #2} {\seq_count:N #3}} {
\seq_put_left:Nx #1 {\int_eval:n {\seq_item:Nn #2 { - ##1} - \seq_item:Nn #3 { - ##1}+0}}
}
\poly_reduce_mod:N #1
}
\cs_generate_variant:Nn \poly_sub:NNN {Ncc,ccc}
\cs_new_nopar:Npn \poly_shift:Nn #1#2 {
\prg_replicate:nn {#2} {
\seq_put_right:Nn #1 {0}
}
}
\cs_new_nopar:Npn \poly_mul:NNN #1#2#3 {
\seq_clear_new:N #1
\group_begin:
\seq_clear_new:N \l__poly_tmpa_seq
\seq_clear_new:N \l__poly_tmpb_seq
\seq_clear_new:N \l__poly_tmpc_seq
\int_set:Nn \l__poly_tmpa_int {\seq_count:N #2 - 1}
\seq_map_inline:Nn #2 {
\seq_clear:N \l__poly_tmpa_seq
\seq_map_inline:Nn #3 {
\seq_put_right:Nx \l__poly_tmpa_seq {\int_eval:n {##1 * ####1}}
}
\poly_shift:Nn \l__poly_tmpa_seq {\l__poly_tmpa_int}
\poly_add:NNN \l__poly_tmpc_seq \l__poly_tmpb_seq \l__poly_tmpa_seq
\seq_set_eq:NN \l__poly_tmpb_seq \l__poly_tmpc_seq
\int_decr:N \l__poly_tmpa_int
}
\seq_gset_eq:NN \l__poly_gtmpa_seq \l__poly_tmpb_seq
\group_end:
\seq_set_eq:NN #1 \l__poly_gtmpa_seq
\seq_clear:N \l__poly_gtmpa_seq
\poly_reduce_mod:N #1
}
\cs_generate_variant:Nn \poly_mul:NNN {Ncc, ccc}
\cs_new_nopar:Npn \poly_int_div:Nnn #1#2#3
{
\int_set:Nn #1 {#2 / #3}
}
\cs_new_nopar:Npn \poly_mod_int_div:Nnn #1#2#3
{
\int_zero:N \l__poly_mod_tmpa_int
\int_set_eq:NN \l__poly_mod_tmpb_int #2
\int_set:Nn \l__poly_mod_tmpc_int { \l__poly_base_int - #3 }
\bool_while_do:nn {
\int_compare_p:n { \l__poly_mod_tmpa_int < \l__poly_base_int }
&&
\int_compare_p:n {\l__poly_mod_tmpb_int != 0 }
}
{
\int_incr:N \l__poly_mod_tmpa_int
\int_set:Nn \l__poly_mod_tmpb_int {
\int_mod:nn { \l__poly_mod_tmpb_int + \l__poly_mod_tmpc_int }
{ \l__poly_base_int }
}
}
\int_set_eq:NN #1 \l__poly_mod_tmpa_int
}
\cs_new_nopar:Npn \poly_div:NNN #1#2#3 {
\seq_clear_new:N #1
\poly_int_div:Nnn \l__poly_tmpa_int {\seq_item:Nn #2 {1} } { \seq_item:Nn #3 {1}}
\seq_put_left:NV #1 \l__poly_tmpa_int
\poly_shift:Nn #1 {\seq_count:N #2 - \seq_count:N #3}
\poly_reduce_mod:N #1
}
\cs_generate_variant:Nn \poly_div:NNN {Ncc, ccc}
\prg_new_conditional:Npnn \poly_is_divisible:NN #1#2 {p,T,F,TF} {
\int_compare:nTF {\seq_count:N #1 < \seq_count:N #2}
{
\prg_return_false:
}
{
\prg_return_true:
}
}
\cs_new_nopar:Npn \poly_trim:N #1 {
\bool_do_while:nn {
\int_compare_p:n {\seq_count:N #1 > 1}
&&
\int_compare_p:n {\seq_item:Nn #1 {1} == 0}
} {
\seq_pop_left:NN #1 \l_tmpa_tl
}
}
\cs_new_nopar:Npn \poly_longdiv:NN #1#2 {
\group_begin:
\seq_clear_new:N \l__poly_quotient_seq
\seq_clear_new:N \l__poly_remainder_seq
\seq_clear_new:N \l__poly_factor_seq
\seq_set_eq:NN \l__poly_remainder_seq #1
\seq_clear_new:N \l__poly_lines_seq
\int_zero:N \l__poly_cstage_int
\bool_do_while:nn {
\poly_is_divisible_p:NN \l__poly_remainder_seq #2
&&
(\l__poly_stage_bool || \int_compare_p:n {\l__poly_stage_int > \l__poly_cstage_int})
}
{
\poly_div:NNN \l__poly_factor_seq \l__poly_remainder_seq #2
\poly_add:NNN \l__poly_tmpa_seq \l__poly_factor_seq \l__poly_quotient_seq
\seq_set_eq:NN \l__poly_quotient_seq \l__poly_tmpa_seq
\poly_mul:NNN \l__poly_tmpa_seq \l__poly_factor_seq #2
\seq_put_right:NV \l__poly_lines_seq \l__poly_tmpa_seq
\int_incr:N \l__poly_cstage_int
\bool_if:nT {\l__poly_stage_bool || \int_compare_p:n
{\l__poly_stage_int > \l__poly_cstage_int}}
{
\poly_sub:NNN \l__poly_tmpb_seq \l__poly_remainder_seq \l__poly_tmpa_seq
\seq_set_eq:NN \l__poly_remainder_seq \l__poly_tmpb_seq
\poly_trim:N \l__poly_remainder_seq
\seq_put_right:NV \l__poly_lines_seq \l__poly_remainder_seq
\int_incr:N \l__poly_cstage_int
}
}
\int_set:Nn \l__poly_pad_int {\seq_count:N #1 + \seq_count:N
#2-1}
\tl_set:Nn \l__poly_sep_tl {&}
\tl_set:Nn \l__poly_longdiv_sep_tl {\cr}
\bool_set_true:N \l__poly_zeros_bool
\int_set:Nn \l__poly_tmpa_int {2*\seq_count:N #1+1}
\tl_set:Nx \l__poly_oline_tl {\exp_not:N\multispan {\int_use:N \l__poly_tmpa_int}\exp_not:N\hrulefill\exp_not:N\cr}
\tl_set:Nx \l__poly_uline_tl {\exp_not:N\multispan {\int_eval:n {2*\seq_count:N #2 -1}}\exp_not:N\hrulefill\exp_not:N\cr}
\tl_set:Nx \l__poly_neguline_tl {\exp_not:N\multispan {\int_eval:n {2*\seq_count:N #2}}\exp_not:N\hrulefill\exp_not:N\cr}
\int_set:Nn \l__poly_trailing_int {\seq_count:N #2}
\leavevmode\vbox{\halign { $##$&&$\>##$ \crcr
&
\bool_if:NTF \l__poly_stage_bool
{
\bool_set_false:N \l__poly_trailing_bool
}
{
\bool_set_true:N \l__poly_trailing_bool
\int_set:Nn \l__poly_trailing_int {\l__poly_stage_int/2}
}
\poly_print:N \l__poly_quotient_seq
\tl_use:N \l__poly_longdiv_sep_tl
\noalign{\vskip-\normalbaselineskip\vskip\jot}
\prg_replicate:nn {2*\seq_count:N #2} {&}
\tl_use:N \l__poly_oline_tl
\int_set:Nn \l__poly_pad_int {0}
\bool_set_true:N \l__poly_trailing_bool
\poly_print:N #2
&
\smash{\!\Bigr)}
&
\int_set:Nn \l__poly_pad_int {0}
\bool_set_false:N \l__poly_trailing_bool
\poly_print:N #1
\tl_use:N \l__poly_longdiv_sep_tl
\int_gzero:N \l__poly_tmpb_int
\seq_map_inline:Nn \l__poly_lines_seq {
\tl_gset:Nn \l__poly_tmpa_seq {##1}
\int_gincr:N \l__poly_tmpb_int
&
\bool_set_true:N \l__poly_trailing_bool
\poly_print:N \l__poly_tmpa_seq
\bool_if:nT {\int_compare_p:n
{\int_mod:nn{\l__poly_tmpb_int}{2} == 1} &&
\int_compare_p:n {
\l__poly_tmpb_int < 2*(\seq_count:N #1 - \seq_count:N #2)
}
&&
\int_compare_p:n {
\l__poly_tmpb_int != \seq_count:N \l__poly_lines_seq
}
} {
&&\hfill\downarrow\hfill
}
\tl_use:N \l__poly_longdiv_sep_tl
\int_compare:nT {\int_mod:nn{\l__poly_tmpb_int}{2} == 1} {
\noalign{\vskip-\normalbaselineskip\vskip\jot}
\int_compare:nNnTF { \seq_item:Nn \l__poly_tmpa_seq 1 } < 0
{
\prg_replicate:nn {2*\seq_count:N #2 + \l__poly_tmpb_int } {&}
\tl_use:N \l__poly_neguline_tl
}
{
\prg_replicate:nn {2*\seq_count:N #2 + \l__poly_tmpb_int + 1} {&}
\tl_use:N \l__poly_uline_tl
}
}
}
\cr
}}
\group_end:
}
\cs_generate_variant:Nn \poly_longdiv:NN {cc}
\NewDocumentCommand \PolyPrint { O{} m } {
\group_begin:
\keys_set:nn { polynomial }
{
#1
}
\poly_print:c {polynomial #2}
\group_end:
}
\NewDocumentCommand \PolySet { m m } {
\seq_set_from_clist:cn {polynomial #1} {#2}
}
\NewDocumentCommand \PolyLongDiv {O{} m m } {
\group_begin:
\keys_set:nn { polynomial }
{
#1
}
\poly_longdiv:cc {polynomial #2} {polynomial #3}
\group_end:
}
\ExplSyntaxOff
\begin{document}
\PolySet{a}{1,-12,0,-42}
\PolySet{b}{1,-3}
\(\PolyLongDiv{a}{b}\)
\PolySet{a}{1,-4,6,-4}
\PolySet{b}{1,-2}
\(\PolyLongDiv{a}{b}\)
\end{document}这个代码作者在github上有仓库: Polynomial-division,用该仓库的代码,余数为0的问题应该已解决。
另一个前面是负号时横线长度是可以解决的,但需要进行较为复杂的逻辑判断,需要判断第一个系数是否为负,根据正负设置\l__poly_uline_tl的起始位置和长度,如:
将\prg_replicate:nn {2*\seq_count:N #2 + \l__poly_tmpb_int + 1} {&}修改为\prg_replicate:nn {2*\seq_count:N #2 + \l__poly_tmpb_int} {&}。
将\tl_put_right:Nx \l__poly_uline_tl {{\int_eval:n {2*\seq_count:N #2 - 1}}}修改为\tl_put_right:Nx \l__poly_uline_tl {{\int_eval:n {2*\seq_count:N #2}}}
但这样简单的修改会带来第一个数为正数时,会产生空白,个人认为进一步修改意义不大。
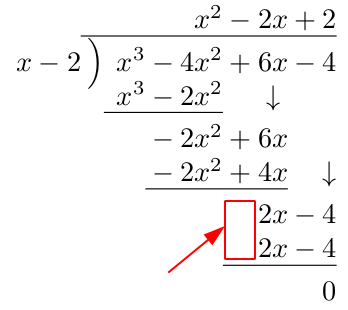







万分感谢!