如何显示公式环境下的点画线
发布于 2022-03-25 22:53:44
已经实现的效果如下:
\documentclass[UTF8,11pt]{ctexart}
\usepackage{amsmath}
\begin{document}
\begin{align*}
&\lim_{x\rightarrow 0} \frac{f\left( e^{x^2} \right) -3f\left( 1+\sin ^2x \right)}{x^2}=\lim_{x\rightarrow 0} \frac{f\left( e^{x^2} \right) -f\left( 1 \right) +3f\left( 1 \right) -3f\left( 1+\sin ^2x \right)}{x^2}
\\
&=\lim_{x\rightarrow 0} \frac{f\left( e^{x^2} \right) -f\left( 1 \right)}{e^{x^2}-1}\frac{e^{x^2}-1}{x^2}-3\lim_{x\rightarrow 0} \frac{f\left( 1+\sin ^2x \right) -f\left( 1 \right)}{\sin ^2x}\frac{\sin ^2x}{x^2}
\\
&\hfill\dotfill\text{ 6分}
\\
&=\lim_{x\rightarrow 0} \frac{f\left( e^{x^2} \right) -f\left( 1 \right)}{e^{x^2}-1}\lim_{x\rightarrow 0} \frac{e^{x^2}-1}{x^2}-3\lim_{x\rightarrow 0} \frac{f\left( 1+\sin ^2x \right) -f\left( 1 \right)}{\sin ^2x}\lim_{x\rightarrow 0} \frac{\sin ^2x}{x^2}
\\
&=f'\left( 1 \right) -3f'\left( 1 \right) =-2f'\left( 1 \right)
\end{align*}
这是一个666的操作\hfill\dotfill6分
\end{document}对应效果为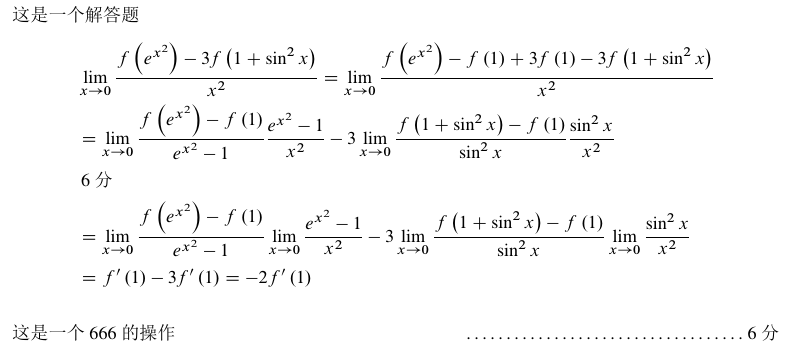
想实现的效果为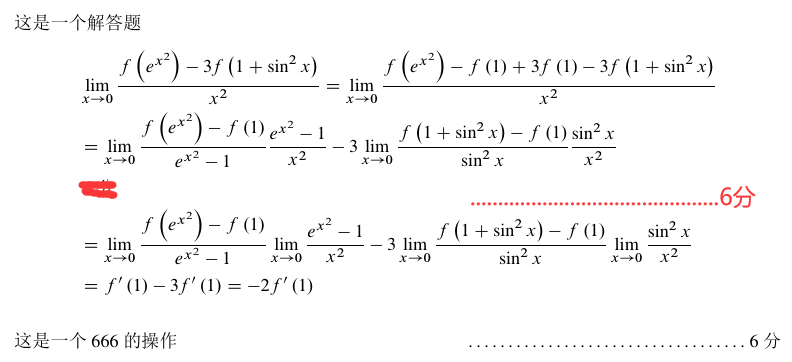
需要如何做呢?
关注者
0
被浏览
1.8k






