关于tkz-euclide宏的“计算与绘制”分离的个人愚见
tkz-euclide在4.0版后,进一步优化了用户接口,更为清晰地实现了“计算与绘制”的分离,并统一了直线、三角形、圆等图形对象的定义方式,从而使代码更为简洁,并且不再依赖于tkz-base宏包。
用tkz-euclide宏包是基于传统尺规绘图的方式进行欧氏几何图形绘制的。它为用户提供了基本的点、线段、直线、三角形、多边形和圆图形对象的定义接口,同时提供了直线与直线、直线与圆和圆与圆求交点的用户接口,从而实现了尺规绘图的基本操作。
基于tkz-euclide宏包,采用“计算与绘制”分离的思想进行欧氏几何图形绘制的基本绘图流程是:
- 定义基础点
- 通过线段、直线、三角形、多边形和圆的定义及求交点的方式,计算得到其它点
- 根据需要绘制图形
- 为图形添加角度、直角、相等线段等标记
- 布置点名称、线段长度、角度值、说明等图形标注
建议:对需要绘制的图形进行必要抽象,尽可能少定义基础点,以便后期图形的修改和变换。
一个用tkz-euclide宏包绘制欧氏几何图形的基本框架是:
\documentclass{standalone}% 可以是任何有效文档类
% 引入tkz-euclide宏包
\usepackage{tkz-euclide}
\begin{document}
% 绘制环境(可以使用任何有效TikZ参数)
\begin{tikzpicture}
% 定义单位圆半径(长度可任意)
\edef\r{2cm}
% 定义基础点(尽可能少)
\tkzDefPoints{0/-2/M, 0/2/N}
% 计算其它点
% 定义直线MN的垂线xx'
\tkzDefLine[mediator](M,N) \tkzGetPoints{x}{x'}
% 求垂足O
\tkzInterLL(M,N)(x,x') \tkzGetPoint{O}
% 求单位圆与x,x'轴的交点
\tkzInterLC[R](x',x)(O,\r) \tkzGetPoints{b}{a}
% 绘制
% 绘制MN和xx'
\tkzDrawLine[dashed, add = 0.05 and 0.05, color = orange!40!black](M,N)
\tkzDrawLine[dashed, add = 0.05 and 0.05, color = orange!40!black](x,x')
% 绘制线段
\tkzDrawSegments(M,N x,x')
% 绘制点
\tkzDrawPoints(M,N,O,x,x')
% 标记
% 添加线段相等标记
\tkzMarkSegments[color=gray,pos=0.5,mark=s|](O,x O,x')
% 标注
% 标各个点的名称
\tkzLabelPoints(x,x')
\tkzLabelPoints[below left](M,N,O)
% 为线段作标注
\tkzLabelSegment[above,sloped,midway](O,x){$1$}
\tkzLabelSegment[above,sloped,midway](O,x'){$1$}
\end{tikzpicture}
\end{document}以下是一个在正五边形内绘制“欧氏蛋”的方法(近似):
\documentclass{standalone}% 可以是任何有效文档类
% 引入tkz-euclide宏包
\usepackage{tkz-euclide}
\begin{document}
% 绘制环境(可以使用任何有效TikZ参数)
\begin{tikzpicture}
% 定义单位圆半径(长度可任意)
\edef\r{2cm}
% 定义基础点(尽可能少)
\tkzDefPoints{0/-2/M, 0/2/N}
% 计算其它点
% 定义垂直平分线并求垂足
\tkzDefLine[mediator](M,N) \tkzGetPoints{x}{x'}
\tkzInterLL(M,N)(x,x') \tkzGetPoint{O}
% 确定正五边形连长
\tkzInterLC[R](x',x)(O,\r) \tkzGetPoints{b}{a}
% 定义正五边形,求得五个顶点
\tkzDefRegPolygon[side,sides=5,name=P](a,b)
% 求对角线交点
\tkzInterLL(P1,P4)(P3,P5) \tkzGetPoint{A}
\tkzInterLL(P2,P4)(P3,P5) \tkzGetPoint{B}
% 求边线上的交点
\tkzInterLC[with nodes](P2,P3)(A,P4,P3) \tkzGetPoints{C}{c}
\tkzInterLC[with nodes](P1,P5)(B,P4,P5) \tkzGetPoints{d}{D}
% 求各直线交点
\tkzInterLL(C,D)(M,N) \tkzGetPoint{O1}
\tkzInterLL(C,D)(P1,P4) \tkzGetPoint{E}
\tkzInterLL(C,D)(P2,P4) \tkzGetPoint{F}
\tkzInterLL(B,D)(A,C) \tkzGetPoint{O2}
\tkzInterLL(P2,P5)(B,D) \tkzGetPoint{K}
\tkzInterLL(P1,P3)(A,C) \tkzGetPoint{J}
% 求欧氏蛋与底边交点
\tkzInterLC(P1,P2)(O1,F) \tkzGetPoints{I}{I'}
% 求欧氏蛋顶点
\tkzInterLC(M,N)(O1,F) \tkzGetPoints{G}{g}
\tkzInterLC(M,N)(O2,A) \tkzGetPoints{h}{H}
% 绘制
% 绘制基础正五边形和需要线段
\tkzDrawPolygon[dashed,fill=cyan!30,draw=blue,fill opacity=0.3](P1,P2,P3,P4,P5)
\tkzDrawSegments[dashed, red!40!black](P1,P4 P1,P3 P2,P4 P2,P5 P3,P5 P4,O E,I)
\tkzDrawSegments[dashed, red!40!black](A,C B,D C,D E,I A,I' B,I)
% 绘制纵轴
\tkzDrawLine[dashed, add = 0.05 and 0.05, color = orange!40!black](G,P4)
% 绘制欧氏蛋
\tkzFillSector[fill=red,fill opacity=0.3](O1,G)(F)
\tkzDrawArc[line width=2pt,draw=red](O1,G)(F)
\tkzFillSector[fill=yellow,fill opacity=0.3](D,F)(B)
\tkzDrawArc[line width=2pt,draw=yellow](D,F)(B)
\tkzFillSector[fill=green,fill opacity=0.3](O2,B)(H)
\tkzDrawArc[line width=2pt,draw=green](O2,B)(H)
\tkzDrawArc[line width=2pt,draw=green](O2,H)(A)
\tkzDrawArc[line width=2pt,draw=yellow](C,A)(E)
\tkzDrawArc[line width=2pt,draw=red](O1,E)(G)
% 绘制点
\tkzSetUpPoint[size = 3]
\tkzDrawPoints(P1,P2,P3,P4,P5,C,D,J,K)
\tkzSetUpPoint[fill = red!50, color = red]
\tkzDrawPoints(O1,O2,D)
\tkzSetUpPoint[fill = white, color = black]
\tkzDrawPoints(H,B,F,G,E,A,I,I')
% 标记
% 标记相等线段
\tkzMarkSegments[color=gray,pos=0.5,mark=s||](E,I O1,O2)
% 标记角
\tkzMarkAngle[size=0.4](P2,P5,P3)
\tkzMarkRightAngle[red,size=0.2](P4,O1,D)
% 标注各点名称
\tkzLabelPoints[above left](P4,P5,H,A,E)
\tkzLabelPoints[above right](B,P3,F)
\tkzLabelPoints[below left](D,P1,G,O1,J,I)
\tkzLabelPoints[below right](P2,C,K,O2,I')
% 标注角度
\tkzLabelAngle[pos=0.7,font=\tiny](P2,P5,P3){$72^\circ$}
% 标注线段长度
\tkzLabelSegment[above,sloped,midway,font=\tiny](P3,P4){$1$}
\tkzLabelSegment[above,sloped,midway,shift={(-20pt,12pt)},font=\tiny](P2,P4){$P2P4=\Phi$}
\tkzLabelSegment[above,sloped,midway,font=\tiny](B,P4){$\Phi-1$}
\tkzLabelSegment[above,sloped,midway,font=\tiny](F,B){$\Phi-1$}
\tkzLabelSegment[above,sloped,midway,font=\tiny](F,P2){$2-\Phi$}
\tkzLabelSegment[above,sloped,midway,font=\tiny](F,O1){$2-\Phi$}
\tkzLabelSegment[above,sloped,midway,font=\tiny](D,K){$2-\Phi$}
\tkzLabelSegment[above,sloped,midway,font=\tiny](K,O2){$2-\Phi$}
\tkzLabelSegment[above,sloped,midway,font=\tiny](O2,B){$2\Phi-3$}
\tkzLabelSegment[below,sloped,midway,font=\tiny](D,E){$2\Phi-3$}
\end{tikzpicture}
\end{document}其绘制结果为:
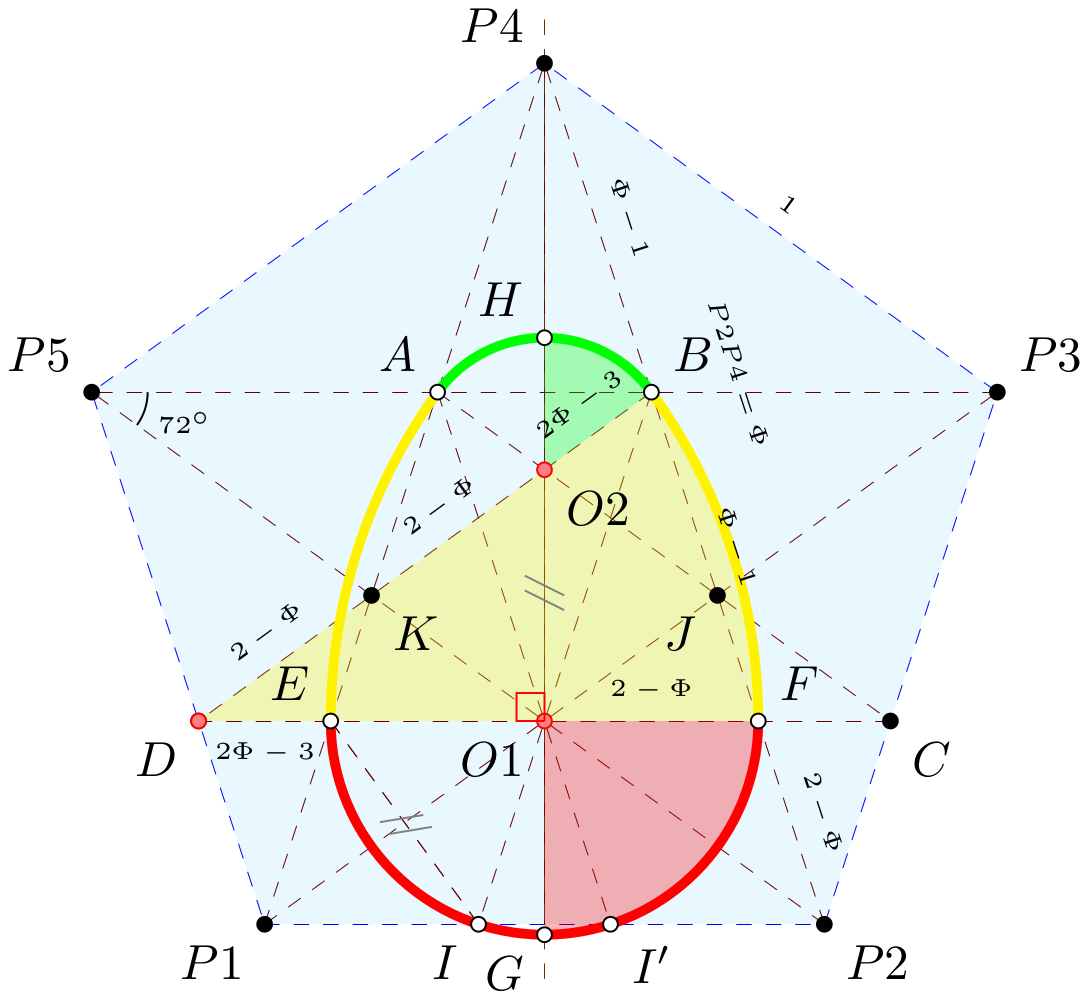
如果需要改变大小方向,则仅需修改单位圆半径长度和MN的方向即可,其它代码可以不作任何改动,如:
...
% 定义单位圆半径(长度可任意)
\edef\r{4cm}
% 定义基础点(尽可能少)
\tkzDefPoints{0/-2/M, 2/2/N}
...其结果为: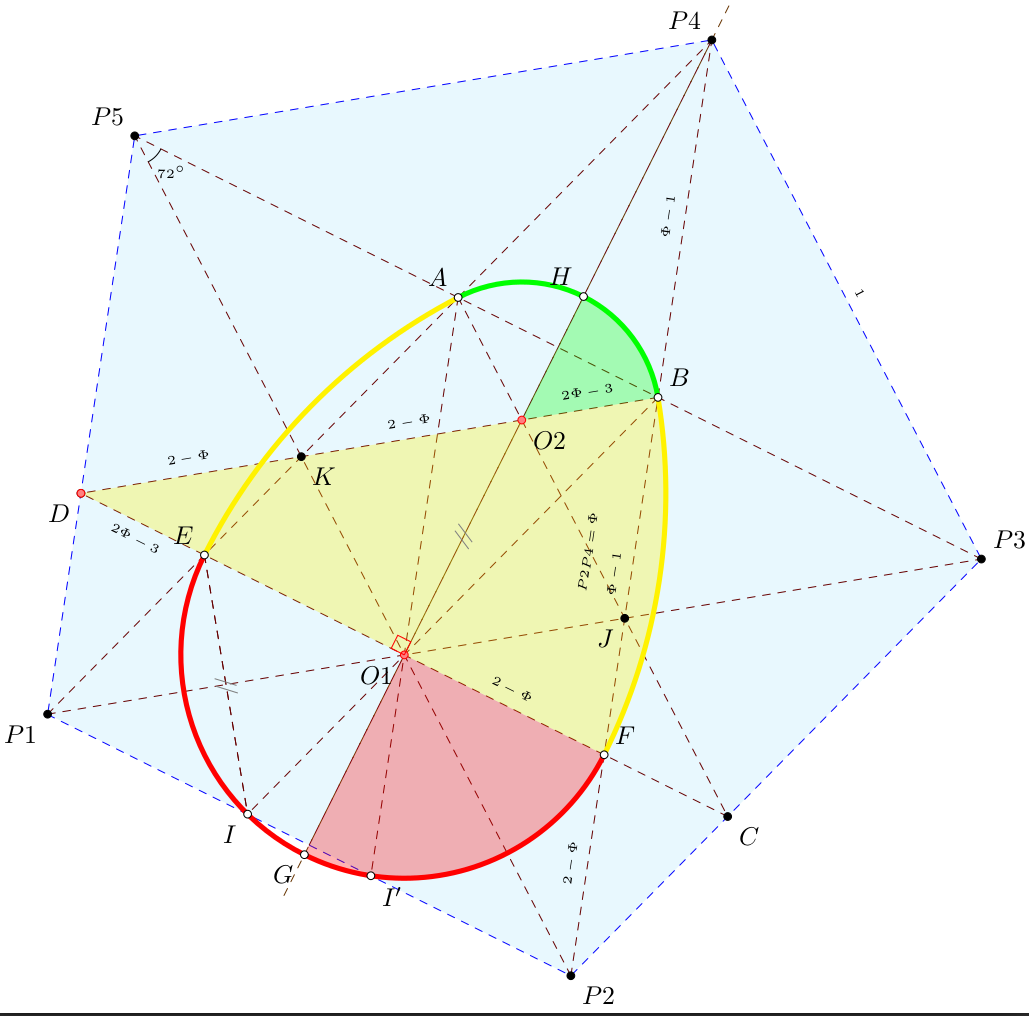
当然,也不必完拘泥于“规范”,如果将角的标记和角度的标注代码放在一起的话,感觉逻辑上会更为清晰:
% 标记和标角
\tkzMarkAngle[size=0.4](P2,P5,P3)
\tkzLabelAngle[pos=0.7,font=\tiny](P2,P5,P3){$72^\circ$}关于tkz-euclide宏包的使用细节,可以在命令行使用texdoc tkz-euclide命令打开其说明书进行查看。
笔者做过该宏包说明书(V3.06c)的翻译,由于时间和精力有限,暂无法再次跟踪翻译其新版说明书。
在tkz-euclide作者的主页,看到作者正在用lua开发一个基于面向对象技术的tkz-elements宏包,将计算与绘制中的计算全部交由lua实现,大家有兴趣了也可以去看看。
在此,附上简单整理的一个tkz-ecuclide5.02C的一个Xmind思维导图,欢迎广大网友批评指正:tkz-euclide-5.02C.zip(敬请解压后用Xmind软件打开)
。






