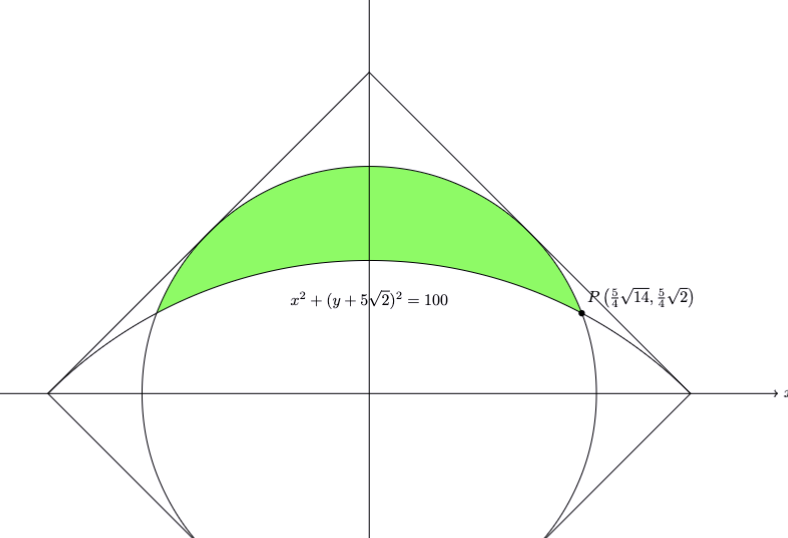
20 如何将两段圆弧的围成的区域染成绿色
发布于 2024-07-12 19:55:55

如何优化代码,实现如图的效果,将阴影区域染成淡蓝色。以下是部分原始代码。
documentclass{standalone}
usepackage{tikz,pgfplots}
usetikzlibrary{arrows.meta}
begin{document}
\begin{tikzpicture}
% Define the coordinates
\coordinate (O1) at (0, {-5*sqrt(2)});
\coordinate (O2) at (0, 0);
% Define the square vertices
\coordinate (A) at (0, {5*sqrt(2)});
\coordinate (B) at ({5*sqrt(2)}, 0);
\coordinate (C) at (0, {-5*sqrt(2)});
\coordinate (D) at ({-5*sqrt(2)}, 0);
% Define point P
\coordinate (P) at ({(5/4)*sqrt(14)}, {(5/4)*sqrt(2)});
% Draw the axes
\draw[->] (-9, 0) -- (9, 0) node[right] {$x$};
\draw[->] (0, -9) -- (0, 9) node[above] {$y$};
% Clip to the region above the x-axis for the first circle
\begin{scope}
\clip (-12, 0) rectangle (12, 15);
% Draw the circle C: x^2 + (y + 5*sqrt(2))^2 = 100, only above x-axis
\draw (O1) circle[radius=10];
\end{scope}
% Draw the circle x^2 + y^2 = 25
\draw (O2) circle[radius=5];
% Draw the square
\draw (A) -- (B) -- (C) -- (D) -- cycle;
% Draw and label point P
\fill (P) circle (2pt);
\node[above right] at (P) {$P\left(\frac{5}{4}\sqrt{14}, \frac{5}{4}\sqrt{2}\right)$};
% Label the circles
\node at (0, {5*sqrt(2) - 5}) {$x^2 + (y + 5\sqrt{2})^2 = 100$};
\node at (0,-5.5) {$x^2 + y^2 = 25$};
\end{tikzpicture}
end{document}
关注者
1
被浏览
1.5k