TA的回答 - 第12页

问 tabularray包可以实现可变列数的表格吗?

\int_step_inline:nn 不能被完全展开，而且 expand 选项只会展开一次，只能使用类似 \int_step_inline:nn {} { \tl_put_right:Nn ... } 的方式将内容存入宏中，然后再在 tblr 中展开这个宏。

\documentclass{ctexart}
\usepackage{tabularray}

\ExplSyntaxOn
% \tl_new:N \l__my_choice_colspec_tl % colspec 选项可要可不要
\tl_new:N \l__my_choice_content_tl
\NewDocumentCommand \choiceTable { +O{} O{1} m m } % tblr options, first num, last num, ...
  {
    % \tl_set:Nx \l__my_choice_colspec_tl { \prg_replicate:nn { #3-#2+2 } { l } } % colspec 选项
    \tl_clear:N \l__my_choice_content_tl
    \tl_put_right:Nn \l__my_choice_content_tl { 题号 }
    \int_step_inline:nnnn {#2} { 1 } {#3}
      { \tl_put_right:Nn \l__my_choice_content_tl { & ##1 } }
    \tl_put_right:Nn \l__my_choice_content_tl { \\ 答案 }
    \tl_put_right:Nx \l__my_choice_content_tl
      { \prg_replicate:nn { #3 - #2 } { & } } % 第二行的 & & & ...
    % \tl_put_right:Nn \l__my_choice_content_tl { \\ } % 最后一个 \\ 可要可不要
    \begin{tblr} [ expand = \l__my_choice_content_tl ] {#1}
      \l__my_choice_content_tl 
    \end{tblr}
  }
\ExplSyntaxOff


\begin{document}

\choiceTable[hlines,vlines]{5}{}

\choiceTable[hlines,vlines][6]{10}{}

\end{document}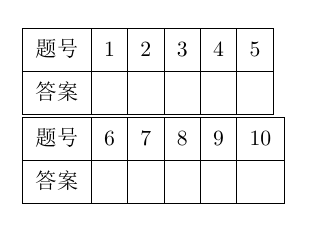

当然，这个实现并不能自动换行，但是也不难实现，只要在适当位置插入 \\ 等内容即可。

1 条评论收藏感谢

问如何解决这个页脚的BUG?

\smallcolorbox 的定义中，删掉 tcolorbox 盒子的 breakable 选项即可（或设置它为 false）。

当 tcolorbox 盒子在另一个盒子中（如 \parbox），breakable 不可用。

另外，\set_wisdom:nn、\add_wisdom:nn、\use_wisdom: 等名称最好改为 \wisdom_set:nn、\wisdom_add:nn、\wisdom_use:，模块名应该在前面。

1 条评论收藏感谢

问网上下载模板用中文编译出错，字体缺失，但自己写的中文却编译成功？

在 structure.tex 文件中，注释掉这一行即可：

%\usepackage{XCharter} % Use the XCharter fonts

使用 XeTeX 编译时，上面两行也可注释掉：

%\usepackage[utf8]{inputenc} % Required for inputting international characters
%\usepackage[T1]{fontenc} % Output font encoding for international characters

1 条评论收藏感谢

问同样的列表环境，用硬编码和 latex3 循环逻辑生成的 item 之间的空白间隔不一致，求大神指导

问题可简化为

\documentclass[zihao=-4]{ctexart}
\usepackage{geometry}
\geometry{a4paper,left=25mm,right=25mm,top=25mm,bottom=25mm, headheight=20mm}

\usepackage{expl3}
\usepackage{tabularx}
\usepackage{layouts}
\ctexset{linestretch=1.245, autoindent=2\ccwd} 
\begin{document}
 
\ExplSyntaxOn

\begin{tabular*}{\linewidth}{p{0.25\linewidth}p{0.25\linewidth}p{0.25\linewidth}p{0.25\linewidth}}
  \int_step_inline:nn { 4 } { A. 5 \int_compare:nNnTF {#1} = { 4 } { \\ } { & } }
\end{tabular*}
\par
????????

\ExplSyntaxOff

\end{document}

实际还可进一步简化，

\begin{tabular}{l}
A \\ \relax
\end{tabular}
\par
???????

上面这个同样会出现“多余的”空行。

其原因是，\relax 是在表格新的一行中。这个表格实际有两行，只不过第二行是空白行。

回到你的问题，实际上，将 \int_step_inline:nn 相应的换成 \int_step_function:nN 则不会出现多余的空行。
这涉及到 \int_step_inline:nn 的内部实现。

为了能够处理嵌套的 ...inline:nn 情况，有一个专门记录嵌套数的 int，它在一个新的嵌套开始前加1，在嵌套完成后减 1。在你的代码中，嵌套完成时的最后一个记号是 \\，在这个记号之后，...inline:nn 还会追加一个减 1 的操作，这操作在 LaTeX 看来，语法上并不属于表格的当前行，因为当前行已经在此前的 \\ 处结束了，它是下一行的内容。自然就会留下一个空白行。

想要移除这个空白行也很简单，方法也很多，如自己定义一个不追加加一减一操作的 ...inline:nn：

\cs_set_protected:Npn \my_int_step_inline:nn #1#2 
  {
    \cs_gset:Npn \__my_tmp:w ##1 {#2} 
    \int_step_function:nN {#1} \__my_tmp:w
  }

这是完全可行的（要注意全局定义 \__my_tmp:w，因为每一个单元格都在一个组中），只是嵌套使用时会有点小问题。

1 条评论收藏感谢

问 texlive2022不能用mtpro2字体了

给出 MWE 以及 log 文件。

是否正确安装了 mtpro2 字体库？

0 条评论收藏感谢

问 \thispagestyle{empty}不能取消页码

\part 的结构为：

\clearpage (\cleardoublepage)
...
\thispagestyle{<pagestyle>}
...
\newpage
...

由于使用了 \clearpage 和 \newpage，使用 \thispagestyle 无法修改 part 页的 pagestyle。
\chapter 则没有尾部的 \newpage，thispagestyle` 可以生效。

如果使用 titlesec 宏包，它提供了 \assignpagestyle 来修改页面样式。如：

\assignpagestyle{\part}{empty}
\assignpagestyle{\chapter}{empty}

将修改 \part 和 \chapter 的 pagestyle 为 empty。此命令应在 \titleformat{<command>}... 后使用。它可以在任意位置使用，将影响其后的 pagestyle。

当使用 ctex 文档类时，可使用 \ctexset{part/pagestyle=..., chapter/pagestyle=...} 直接设置 pagestyle。但当加载 titlesec 后无效。

对于本例，若要全局修改，只需在导言区使用：

%\usepackage{titlesec}
\titleformat{\part}[display]{\Huge\bf}{第\thepart 部分}{1em}{}
\assignpagestyle{\part}{empty}

若只修改个别，则

\assignpagestyle{\part}{empty}
\part{...}
\assignpagestyle{\part}{plain} % 改回来，默认为 plain

0 条评论收藏感谢

问如何让TColorBox中，标题的脚注和内容的脚注，显示在一起？

tcolorbox 的每个块默认是单独放在一个 minipage 中的，如果要实现这样的需求，必须使用 \footnotemark 和 \footnotetext 单独设置。

...[title={title\footnotemark}]...

\footnotetext{foot1}

但这样的话标题中的脚注标记与 upper 部分中的标记不同，为此，可以使用 nccfoots 宏包提供的
\Footnotemark 和 \Footnotetext 来设置脚注标记符号。

\documentclass[11pt,twocolumn]{ctexart}
\usepackage{tcolorbox}
\usepackage{nccfoots}
\begin{document}
\begin{tcolorbox}[%colbacktitle=black!10!white,
    title=title\Footnotemark{a}]
\footnotetext[1]{foot1}
    content\footnote[2]{foot2}
\end{tcolorbox}
\end{document}

0 条评论收藏感谢

问 tcolorbox中插入图片

使用 caption 宏包提供的 \captionof 命令，可在非浮动体中生成相应的 caption。

\documentclass{article}
\usepackage{caption}
\usepackage{tcolorbox}
\usepackage{hyperref}

\begin{document}

\begin{tcolorbox}
\begin{center}
\includegraphics[width=3cm]{example-image-golden}
\captionof{figure}{test}\label{fig:1}
\end{center}
\end{tcolorbox}

\ref{fig:1}
\end{document}

0 条评论收藏感谢

问 clist使用方法请教

tl、str、clist、seq、prop 等类型都有对应的 map 函数，

\..._map_function:NN <data> <func>
\..._map_tokens:Nn   <data> <tokens>
\..._map_inline:Nn   <data> <code>

它们将 <func>、<tokens> 作用于 <data> 的每一项，也即，在 <data> 的每一项前添加 <func>、<tokens>，变成：

<func> <item1> <func> <item2> <func> <item3> ...

<tokens> <item1> <tokens> <item2> <tokens> <item3> ...

对于 \..._map_inline:Nn 则是先将一个 <temp func> 定义为 <code>，它可使用一个参数，代表当前的 item。再对 <temp func> 使用 \..._map_function:NN。

你这个可以用 \tl_map_inline:nn，或者 \clist_map_inline:nn，前者速度更快：

\tl_map_inline:nn { ABCD }
  {
    \exp_args:Nc \NewDocumentCommand { xxColor #1 } { } 
      {
        \bool_lazy_and:nnTF
          { \bool_not_p:n \l_choice_隐藏答案_bool }
          { \use:c { l_choice_ #1 _bool } }
          { { \color{red} \bfseries #1 . } }
          { #1 . }
      }
  }

1 条评论收藏感谢

问关于底纹颜色和大小的一个问题

\documentclass{ctexart}
\usepackage{zhlipsum}
\usepackage{niceframe}
\usepackage{dingbat}
\usepackage{bbding}
\usepackage{tikz}
\usepackage[margin=2cm]{geometry}

\makeatletter
\newlength\this@pgf@bop@width
\newlength\this@pgf@bop@height
\def\this@pgf@bop@color{black}
\def\this@pgf@bop@opacity{1}
\def\this@pgf@bop@xscale{1}
\def\this@pgf@bop@yscale{1}
\ExplSyntaxOn
\cs_new_protected:Npn \this@pgf@bop@setscale #1
  {
    \box_scale:cnn { this@pgf@box@pattern #1 }
      { \this@pgf@bop@xscale } { \this@pgf@bop@yscale }
    \tl_set:cx { this@pgf@bop@#1@width } { \box_wd:c { this@pgf@box@pattern#1 } }
    \tl_set:cx { this@pgf@bop@#1@height } { \box_ht_plus_dp:c { this@pgf@box@pattern#1 } }
  }
\ExplSyntaxOff

\def\setboxaspattern#1#2{\expandafter\newbox\csname this@pgf@box@pattern#1\endcsname
  \expandafter\setbox\csname this@pgf@box@pattern#1\endcsname\hbox{#2}%
  \expandafter\edef\csname this@pgf@bop@#1@width\endcsname{\the\wd\csname this@pgf@box@pattern#1\endcsname}%
  \expandafter\edef\csname this@pgf@bop@#1@height\endcsname{\the\dimexpr\ht\csname this@pgf@box@pattern#1\endcsname+\dp\csname this@pgf@box@pattern#1\endcsname}%
}
\tikzset{
  box pattern xscale/.code={\def\this@pgf@bop@xscale{#1}},
  box pattern yscale/.code={\def\this@pgf@bop@yscale{#1}},
  box pattern scale/.code={\def\this@pgf@bop@xscale{#1}\def\this@pgf@bop@yscale{#1}},
  box pattern color/.code={\def\this@pgf@bop@color{#1}},
  box pattern opacity/.code={\def\this@pgf@bop@opacity{#1}},
  box as pattern/.code 2 args={%
    \this@pgf@bop@setscale{#2}%
    \expandafter\this@pgf@bop@width\csname this@pgf@bop@#2@width\endcsname
    \expandafter\this@pgf@bop@height\csname this@pgf@bop@#2@height\endcsname
    \pgfkeysalso{/tikz/path picture={%
      \pgf@process{\pgfpointanchor{path picture bounding box}{north east}}%
      \pgf@xa\pgf@x \pgf@ya\pgf@y
      \pgf@process{\pgfpointanchor{path picture bounding box}{south west}}%
      \pgf@xb\pgf@x \pgf@yb\pgf@y \pgf@yc\pgf@yb
      \pgfutil@loop
        {%
        \pgfutil@loop
          \expandafter\pgftext\expandafter[#1,at=\pgfqpoint{\pgf@xb}{\pgf@yb}]{%
            \pgfsetfillcolor{\this@pgf@bop@color}%
            \pgfsetfillopacity{\this@pgf@bop@opacity}%
            \copy\csname this@pgf@box@pattern#2\endcsname}%
          \ifdim\pgf@yb<\pgf@ya
          \advance\pgf@yb\this@pgf@bop@height
        \pgfutil@repeat
        }%
        \ifdim\pgf@xb<\pgf@xa
        \advance\pgf@xb\this@pgf@bop@width
        \pgf@yb\pgf@yc
      \pgfutil@repeat
    }}%
  }
}
\makeatother

\setboxaspattern{hua}{\FourClowerOpen}

\usepackage[many]{tcolorbox}
\usetikzlibrary{decorations,decorations.markings}
\begin{document}
\font\border=karta15
\generalframe
 {\border\char'307}{\border\char'324}{\border\char'322}
 {\border\char'310} {\border\char'323}
 {\border\char'174}{\border\char'325}{\border\char'175}
 {\noindent\tikz\node[box pattern opacity=0.4, box as pattern={}{hua}]
   {\parbox{\dimexpr\textwidth-40pt-4\fboxsep}{\parindent=2\ccwd \zhlipsum[1][name=zhufu]}};}

{\setlength\fboxsep{0pt}
\generalframe
 {\border\char'307}{\border\char'324}{\border\char'322}
 {\border\char'310} {\border\char'323}
 {\border\char'174}{\border\char'325}{\border\char'175}
 {\parindent=0pt
   \begin{tcolorbox}[width=\textwidth-3.28em-4\fboxsep,left=2mm,right=2mm,enhanced,nobeforeafter,
     frame empty,
     interior code={\path[draw=white,fill=white,box pattern opacity=0.3, box as pattern={}{hua}]
     (interior.south west) rectangle (interior.north east);},
  ]
    \parindent=2\ccwd
    \zhlipsum[1][name=zhufu]
  \end{tcolorbox}}}

\makeatletter
\tcbset{arrow frame decoration/.style={
  frame empty,
  before skip=1em plus 5pt, after skip=1em plus 5pt,
     overlay={%
       \draw[decorate,decoration={
         markings, mark=between positions 0.07 and 0.97 step 1.2em with
           {\pgftext{\border\char'325}}}](frame.north west)--(frame.south west);
       \draw[decorate,decoration={
         markings, mark=between positions 0.07 and 0.97 step 1.2em with
           {\pgftext{\border\char'324}}}](frame.north east)--(frame.south east);
       \draw[decorate,decoration={
         markings, mark=between positions 0.03 and 0.97 step {\dimexpr\kvtcb@width/(\numexpr\linewidth/\dimexpr1.5em\relax)} with 
           {\pgftext{\border\char'324}}}](frame.north west)--(frame.north east);
       \draw[decorate,decoration={
         markings, mark=between positions 0.03 and 0.97 step {\dimexpr\kvtcb@width/(\numexpr\linewidth/\dimexpr1.5em\relax)} with 
           {\pgftext{\border\char'325}}}](frame.south west)--(frame.south east);
       \path node at([yshift=-.2ex]frame.south west) {\border\char'174}
             node at([yshift=-.2ex]frame.south east) {\border\char'175}
             node at([yshift=-.2ex]frame.north west) {\border\char'307}
             node at([yshift=-.2ex]frame.north east) {\border\char'322};
     },
},}
\makeatother

\newtcolorbox{arrowframe}[2][]{left=2mm,right=2mm,enhanced,arrow frame decoration,
     interior code={\path[draw=white,fill=white,
       box pattern opacity=.5,box pattern color=red,box pattern scale=1.5,
       box as pattern={}{#2}]
       ([xshift=1ex,yshift=1ex]interior.south west) rectangle
       ([xshift=-1ex,yshift=-1ex]interior.north east);},#1}

\begin{arrowframe}{hua}
    \parindent=2\ccwd
    \zhlipsum[1]
\end{arrowframe}

\end{document}

5 条评论收藏感谢

问关于diagbox宏包画表格线的一个问题

你可以用 nicematrix，它能够使用 tikz 绘制复杂表格（不能跨页）。

\documentclass{ctexart}
\usepackage{xcolor}
\usepackage{tikz}
\usepackage{nicematrix}
\usetikzlibrary{intersections,patterns,decorations.pathmorphing}

\begin{document}

\begin{NiceTabular}{>{\centering}p{2cm}p{2cm}p{2cm}c}[hvlines,
  create-large-nodes,left-margin,right-margin]
\Block{2-3}{~} & & & 什么？\\
~ &~ &~ & \Block{1-1}{wh\\at?} \\
1 & 2 & 3 & 4
\CodeAfter
  \begin{tikzpicture}
  \draw[pattern=north west lines] ([xshift=-1em,yshift=1em]3-4-large.north west) rectangle ([xshift=1pt,yshift=-.5pt]3-4-large.south east);
  \path[fill=red!30] ([xshift=1em-1pt]1-1-large.north west) arc (0:-90:1em) --([xshift=-1pt]1-1-large.north west) --cycle;
  \draw (1-1-large.north west)-- node[midway,below left=-2pt]{看看} (2-2-large.south west);
  \draw[decorate,decoration={snake}] (1-1-large.north west)-- node[pos=0.6,below left=-2.5pt]{第二} (2-3-large.south west);
  \draw (1-1-large.north west)-- node[near end,below left]{上下} (1-4-large.south west);
  \path[name path=a] (1-1-large.north west)--(2-4-large.south west);
  \draw[name path=b] (3-3-large.north west)--(1-4-large.south west);
  \draw[name intersections={of=a and b, name=itr}] (itr-1)-- node[pos=.4,above right=-2pt]{what} (3-4-large.north west);
  \draw[dashed] (1-1-large.north west)--(itr-1);
  \draw (itr-1)--(3-1-large.north west);
  \end{tikzpicture}
\end{NiceTabular}

\end{document}

3 条评论收藏感谢

问关于表格画十字线的一个问题

tabularray 并不自动展开表格内容，因此，\multicolumn 并未生效。理论上，只要展开 \notableentry 即可，但 \vadjust 不可用。

解决方法建议问宏包作者：issue、discussion。

0 条评论收藏感谢

问 tabularray包可以实现可变列数的表格吗?

问如何解决这个页脚的BUG?

问网上下载模板用中文编译出错，字体缺失，但自己写的中文却编译成功？

问 tikz 手册上的一个绘图示例问题

问关于使用 foreach 语法绘制一些 node 的问题

问有偿定制文本框,用于定理类环境,或者单独的盒子也行!

问同样的列表环境，用硬编码和 latex3 循环逻辑生成的 item 之间的空白间隔不一致，求大神指导

问 texlive2022不能用mtpro2字体了

问 \thispagestyle{empty}不能取消页码

问如何让TColorBox中，标题的脚注和内容的脚注，显示在一起？

问 tcolorbox中插入图片

问 clist使用方法请教

问关于底纹颜色和大小的一个问题

问关于diagbox宏包画表格线的一个问题

问关于表格画十字线的一个问题

会员统计