draw[rotate=45]表示你把椭圆的线旋转了,但是切线没动,要想相对静止,应该考虑整体!
\documentclass[border=2pt]{standalone}
\usepackage{tikz}
\usepackage{xcolor}
\begin{document}
\begin{tikzpicture}
\foreach \N in {0,3,...,360}{
\draw (2,0) arc (0:\N:2 and 1)
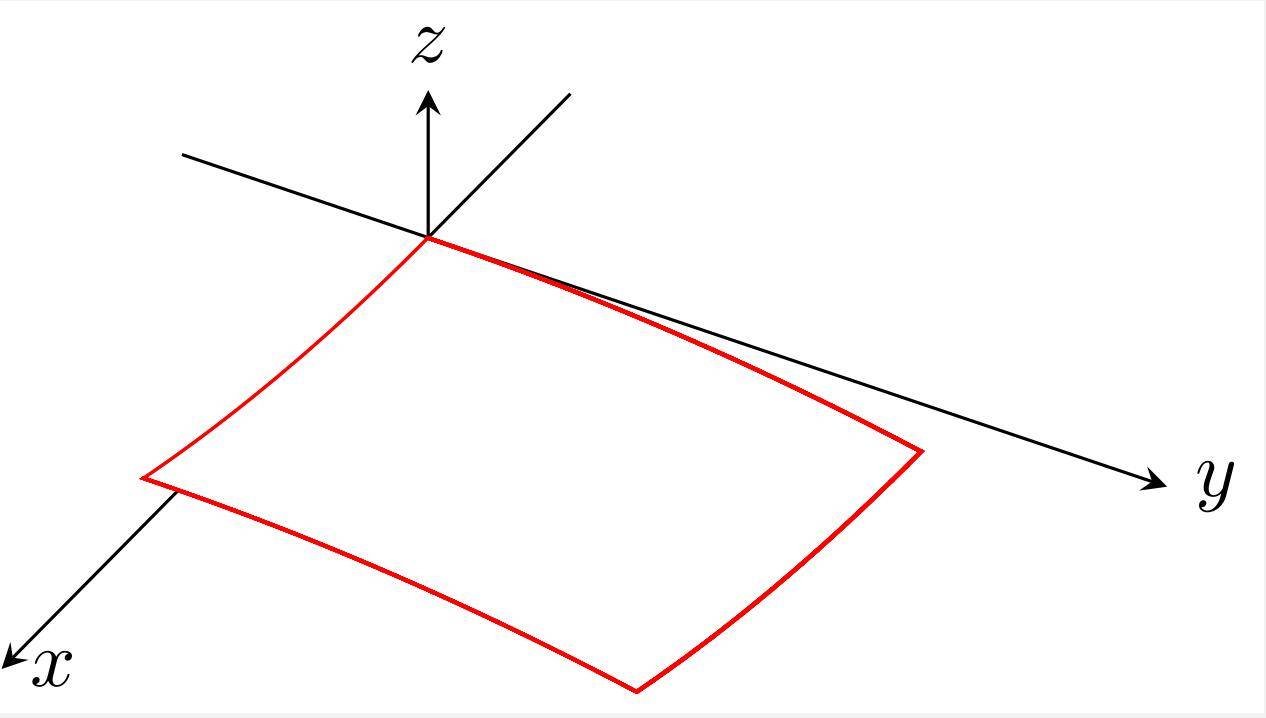
node[
pos = 0.8, % 设置切点在曲线上的位置
sloped, % 设置node按曲线斜率旋转
anchor = south west, % node的锚点设为左下角,即以此为切点
fill opacity = 0.4, % 将node填充为灰色半透明图形,与切线绘制无关
fill = gray % 将node填充为灰色半透明图形,与切线绘制无关
] (N) {};
% 绘制切线(红色)
\draw[red] (N.south west) -- (N.south east);
% 绘制法线(蓝色)
\draw[blue] (N.south west) -- (N.north west);
}
\end{tikzpicture}
\end{document} 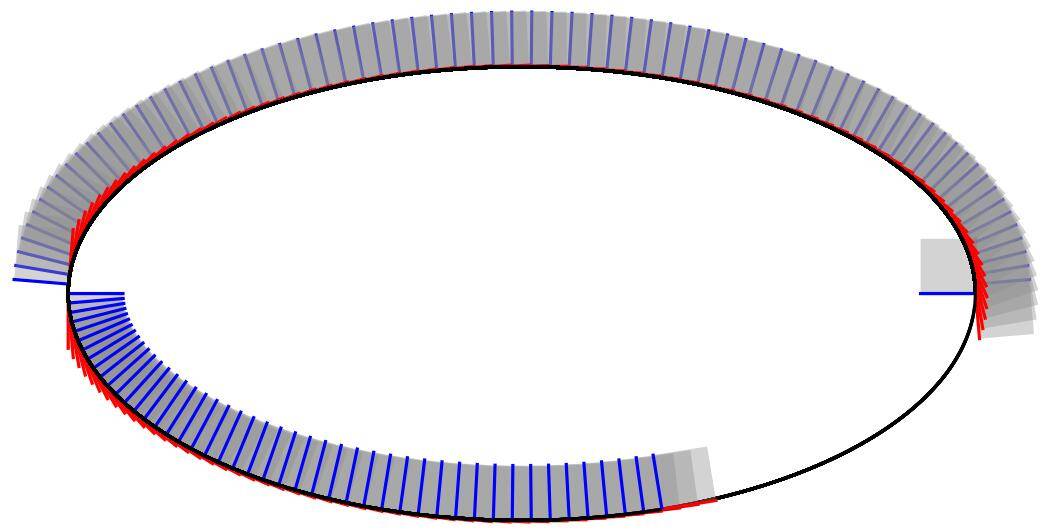


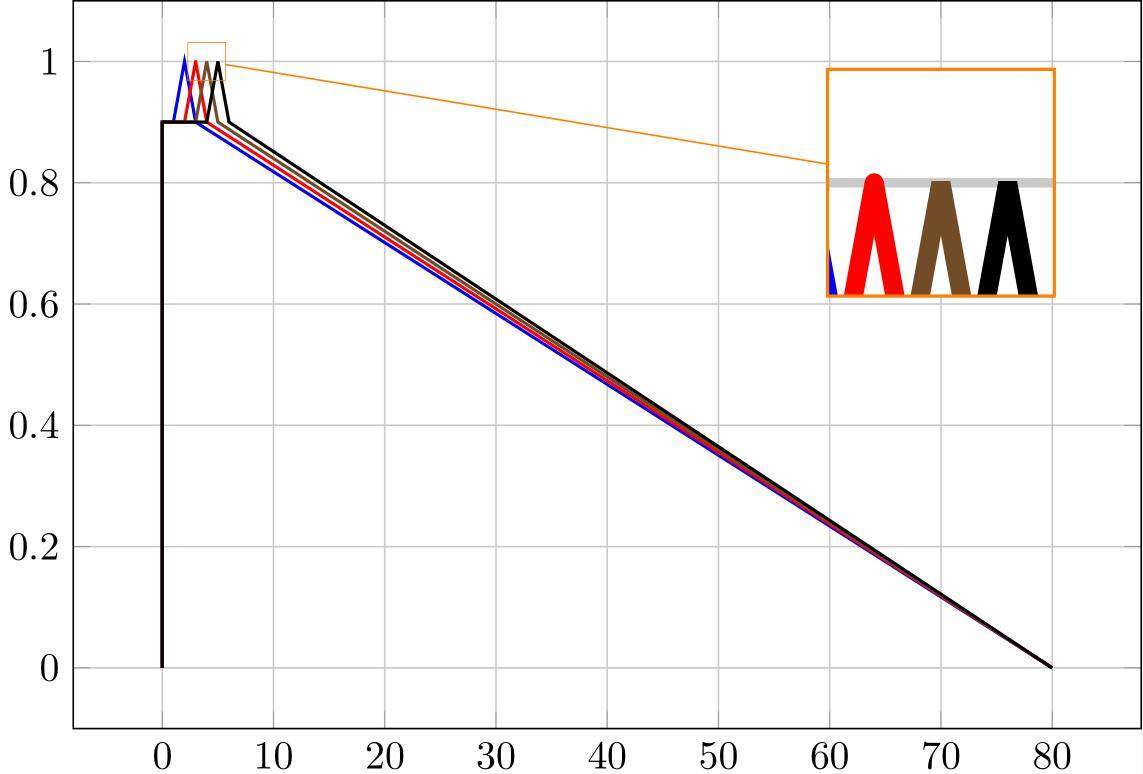
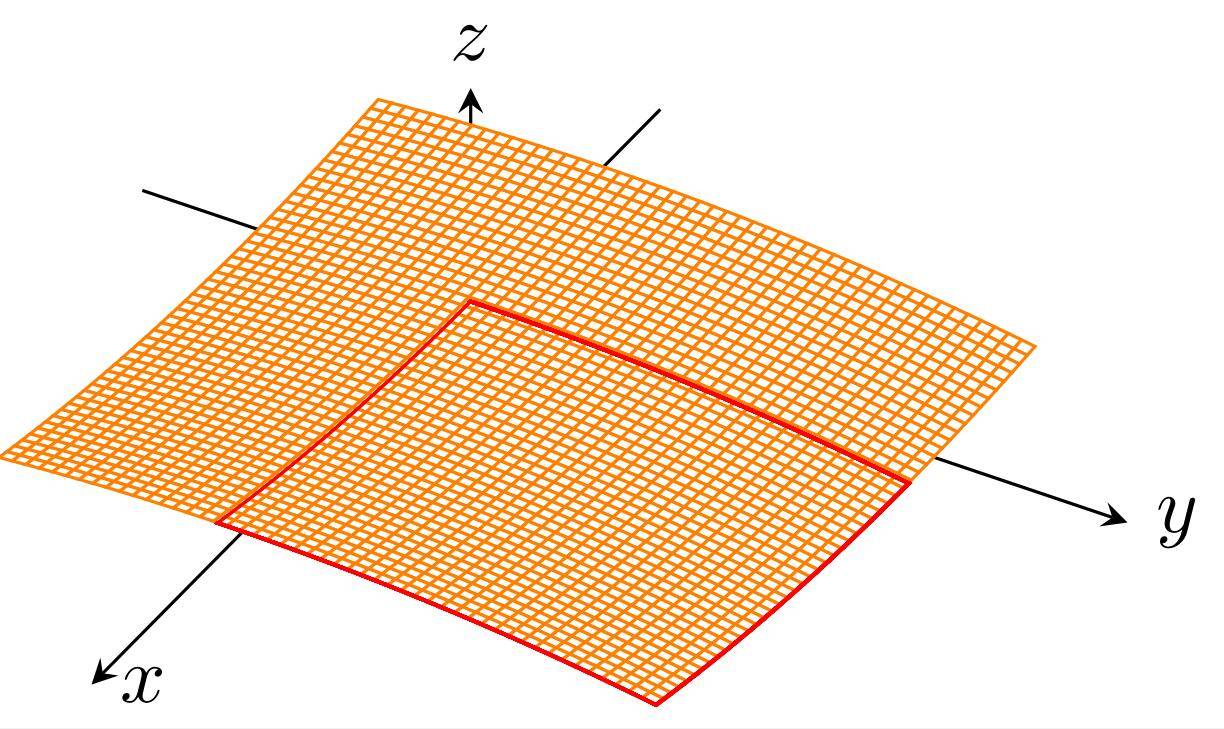





问 如何让node的sloped角度随着弧线转动?