关注者
2
被浏览
5.9k
\documentclass{ctexart}
\usepackage[many]{tcolorbox}
\newcounter{example}[section]
\tcbset{
inbox/.style = {
left = 0.5mm,
right = 0.5mm,
top = -0.5mm,
bottom = -0.5mm,
enhanced,
boxrule = -1pt,
colback = blue!80,
on line,
overlay = {
\draw [blue!80] (frame.west) -- ++ (-0.24cm,0);
}
},
outbox/.style = {
middle = 0mm,
segmentation hidden,
colback = white,
arc = 0mm,
enhanced,
overlay = {
\draw [blue!80] ([yshift=-1.358mm]frame.north west) -- (frame.south west)node[circle,draw,fill,inner sep=1.2pt,anchor=north]{};
},
boxrule = -0.1mm,
enforce breakable,
left = 1.5mm,
top = -1.3mm,
bottom = -1mm,
right = 0mm
}
}
\newcommand\example{
\refstepcounter{example}
\tcbox[inbox] { \color{white}例 \arabic{example} }\quad
\label{exam\arabic{section}.\arabic{example}}
}
\newcommand\solution{
\tcbox[inbox]{\color{white}解} \quad
}
\usepackage[colorlinks]{hyperref}
\begin{document}
\section{第一节}
\begin{tcolorbox}[outbox]
\example 计算
\[
(a + b)(a - b) .
\]
\tcblower
\solution 这是例 \ref{exam1.1} 的解答.
\[
(a + b)(a - b) = a^2 - b^2.
\]
\end{tcolorbox}
\end{document} 
这个可以修改一下王老师给的模板:
\documentclass{ctexart}
\usepackage{tcolorbox}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{mathrsfs}
\tcbuselibrary{breakable,theorems,skins}
\definecolor{Back}{RGB}{70,87,121}
\newcounter{reidaibangou}
\newtcolorbox{reidai}[1][]{enhanced,boxrule=0.5mm,
top=2pt,left=2pt,right=4pt,bottom=2pt,arc=0mm,
colframe=white,
boxrule=1pt,
underlay={
\node[inner sep=1pt,white,fill=Back]at ([xshift=26pt,yshift=-8pt]interior.north west) {\stepcounter{reidaibangou}\sffamily 例~\thereidaibangou};
\draw[Back,line width=1pt]([xshift=0pt,yshift=-8pt]interior.north west)--([xshift=-327pt,yshift=-8pt]interior.north east);
\draw[Back,line width=1pt]([xshift=0pt,yshift=2pt]interior.south west)--(interior.north west);},
segmentation code={
\draw[line width=1pt,Back] ([xshift=0pt,yshift=-14pt]segmentation.west)--([xshift=-325pt,yshift=-14pt]segmentation.east);
\node[inner sep=1pt,white,fill=Back] at ([xshift=24pt,yshift=-8pt]segmentation.south west) {\sffamily 解};},
before upper={\setlength{\parindent}{4\ccwd}},
before lower={\setlength{\parindent}{4\ccwd}},
}
\newcounter{reidaibangouA}
\newtcolorbox{reidaiA}[1][]{enhanced,boxrule=0.5mm,
top=2pt,left=2pt,right=4pt,bottom=2pt,arc=0mm,
colframe=white,
boxrule=1pt,
underlay={
\node[inner sep=1pt,white,fill=Back]at ([xshift=26pt,yshift=-8pt]interior.north west) {\stepcounter{reidaibangou}\sffamily 例~\thereidaibangou};
\draw[Back,line width=1pt]([xshift=0pt,yshift=-8pt]interior.north west)--([xshift=-327pt,yshift=-8pt]interior.north east);
\draw[Back,line width=1pt]([xshift=0pt,yshift=2pt]interior.south west)--([xshift=0pt,yshift=-8pt]interior.north west);},
segmentation code={
\draw[line width=1pt,Back] ([xshift=0pt,yshift=-14pt]segmentation.west)--([xshift=-325pt,yshift=-14pt]segmentation.east);
\node[inner sep=1pt,white,fill=Back] at ([xshift=24pt,yshift=-8pt]segmentation.south west) {\sffamily 解};},
before upper={\setlength{\parindent}{4\ccwd}},
before lower={\setlength{\parindent}{4\ccwd}},
}
\newcounter{reidaibangouB}
\newtcolorbox{reidaiB}[1][]{enhanced,boxrule=0.5mm,
top=2pt,left=2pt,right=4pt,bottom=2pt,arc=0mm,
colframe=white,
boxrule=1pt,
underlay={
\node[inner sep=1pt,white,fill=Back]at ([xshift=26pt,yshift=-8pt]interior.north west) {\stepcounter{reidaibangou}\sffamily 例~\thereidaibangou};
\draw[Back,line width=1pt]([xshift=0pt,yshift=-8pt]interior.north west)--([xshift=-327pt,yshift=-8pt]interior.north east);
\draw[Back,line width=1pt]([xshift=0pt,yshift=0pt]interior.south west)--([xshift=0pt,yshift=-8pt]interior.north west);
\draw[Back,line width=1pt]([xshift=0pt,yshift=0pt]interior.south west)--([xshift=-327pt,yshift=0pt]interior.south east);},
segmentation code={
\draw[line width=1pt,Back] ([xshift=0pt,yshift=-14pt]segmentation.west)--([xshift=-325pt,yshift=-14pt]segmentation.east);
\node[inner sep=1pt,white,fill=Back] at ([xshift=24pt,yshift=-8pt]segmentation.south west) {\sffamily 解};},
before upper={\setlength{\parindent}{4\ccwd}},
before lower={\setlength{\parindent}{4\ccwd}},
}
\begin{document}
\begin{reidai}
求 $\dfrac{(1+i)^3(\sqrt{3}-1\i)}{1+\sqrt{3}i}$
\tcblower 因为
\[
1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)
\]
\[
\sqrt{3}-i=2\left(\cos\left(-\frac{\pi}{6}\right)+i\sin \left(-\frac{\pi}{6}\right)\right)
\]
\[
1+\sqrt{3}i=2\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)
\]
所以
$\begin{array}{l}
\text{原式}=\frac{(\sqrt{2})^3\times 2}{2}\left[\cos\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)+i\sin\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)\right] \\
\hspace{0.85cm}=2\sqrt{2}(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4})\\
\hspace{0.85cm}=2+2i
\end{array}$
\end{reidai}
\begin{reidaiA}
求 $\dfrac{(1+i)^3(\sqrt{3}-1\i)}{1+\sqrt{3}i}$
\tcblower 因为
\[
1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)
\]
\[
\sqrt{3}-i=2\left(\cos\left(-\frac{\pi}{6}\right)+i\sin \left(-\frac{\pi}{6}\right)\right)
\]
\[
1+\sqrt{3}i=2\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)
\]
所以
$\begin{array}{l}
\text{原式}=\frac{(\sqrt{2})^3\times 2}{2}\left[\cos\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)+i\sin\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)\right] \\
\hspace{0.85cm}=2\sqrt{2}(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4})\\
\hspace{0.85cm}=2+2i
\end{array}$
\end{reidaiA}
\begin{reidaiB}
求 $\dfrac{(1+i)^3(\sqrt{3}-1\i)}{1+\sqrt{3}i}$
\tcblower 因为
\[
1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)
\]
\[
\sqrt{3}-i=2\left(\cos\left(-\frac{\pi}{6}\right)+i\sin \left(-\frac{\pi}{6}\right)\right)
\]
\[
1+\sqrt{3}i=2\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)
\]
所以
$\begin{array}{l}
\text{原式}=\frac{(\sqrt{2})^3\times 2}{2}\left[\cos\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)+i\sin\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)\right] \\
\hspace{0.85cm}=2\sqrt{2}(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4})\\
\hspace{0.85cm}=2+2i
\end{array}$
\end{reidaiB}
\end{document} 最后我们得到如下效果,当然也可以根据自己的要求随意修改。
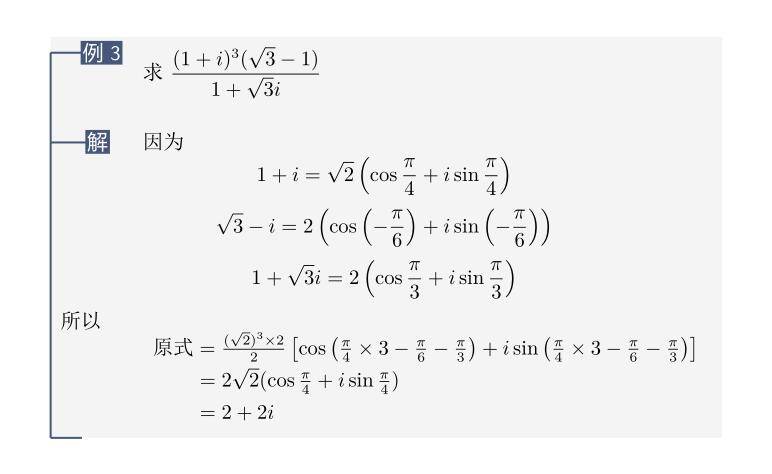
稍作了修正:
\documentclass{ctexart}
\usepackage{tcolorbox}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{mathrsfs}
\tcbuselibrary{breakable,theorems,skins}
\definecolor{Back}{RGB}{70,87,121}
\newcounter{reidaibangou}
\newtcolorbox{reidai}[1][]{enhanced,boxrule=0.5mm,
top=2pt,left=2pt,right=4pt,bottom=2pt,arc=0mm,
colframe=white,
boxrule=1pt,
underlay={
\node[inner sep=1pt,white,fill=Back]at ([xshift=26pt,yshift=-16pt]interior.north west) {\stepcounter{reidaibangou}\sffamily 例~\thereidaibangou};
\draw[Back,line width=1pt]([xshift=0pt,yshift=-16pt]interior.north west)--([xshift=-327pt,yshift=-16pt]interior.north east);
\draw[Back,line width=1pt]([xshift=0pt,yshift=2pt]interior.south west)--(interior.north west);},
segmentation code={
\draw[line width=1pt,Back] ([xshift=0pt,yshift=-14pt]segmentation.west)--([xshift=-325pt,yshift=-14pt]segmentation.east);
\node[inner sep=1pt,white,fill=Back] at ([xshift=24pt,yshift=-8pt]segmentation.south west) {\sffamily 解};},
before upper={\setlength{\parindent}{3.5\ccwd}},
before lower={\setlength{\parindent}{3.5\ccwd}},
}
\newcounter{reidaibangouA}
\newtcolorbox{reidaiA}[1][]{enhanced,boxrule=0.5mm,
top=2pt,left=2pt,right=4pt,bottom=2pt,arc=0mm,
colframe=white,
boxrule=1pt,
underlay={
\node[inner sep=1pt,white,fill=Back]at ([xshift=26pt,yshift=-16pt]interior.north west) {\stepcounter{reidaibangou}\sffamily 例~\thereidaibangou};
\draw[Back,line width=1pt]([xshift=0pt,yshift=-16pt]interior.north west)--([xshift=-327pt,yshift=-16pt]interior.north east);
\draw[Back,line width=1pt]([xshift=0pt,yshift=2pt]interior.south west)--([xshift=0pt,yshift=-16pt]interior.north west);},
segmentation code={
\draw[line width=1pt,Back] ([xshift=0pt,yshift=-14pt]segmentation.west)--([xshift=-325pt,yshift=-14pt]segmentation.east);
\node[inner sep=1pt,white,fill=Back] at ([xshift=24pt,yshift=-8pt]segmentation.south west) {\sffamily 解};},
before upper={\setlength{\parindent}{3.5\ccwd}},
before lower={\setlength{\parindent}{3.5\ccwd}},
}
\newcounter{reidaibangouB}
\newtcolorbox{reidaiB}[1][]{enhanced,boxrule=0.5mm,
top=2pt,left=2pt,right=4pt,bottom=2pt,arc=0mm,
colframe=white,
boxrule=1pt,
underlay={
\node[inner sep=1pt,white,fill=Back]at ([xshift=26pt,yshift=-16pt]interior.north west) {\stepcounter{reidaibangou}\sffamily 例~\thereidaibangou};
\draw[Back,line width=1pt]([xshift=0pt,yshift=-16pt]interior.north west)--([xshift=-327pt,yshift=-16pt]interior.north east);
\draw[Back,line width=1pt]([xshift=0pt,yshift=0pt]interior.south west)--([xshift=0pt,yshift=-16pt]interior.north west);
\draw[Back,line width=1pt]([xshift=0pt,yshift=0pt]interior.south west)--([xshift=-327pt,yshift=0pt]interior.south east);},
segmentation code={
\draw[line width=1pt,Back] ([xshift=0pt,yshift=-14pt]segmentation.west)--([xshift=-325pt,yshift=-14pt]segmentation.east);
\node[inner sep=1pt,white,fill=Back] at ([xshift=24pt,yshift=-8pt]segmentation.south west) {\sffamily 解};},
before upper={\setlength{\parindent}{3.5\ccwd}},
before lower={\setlength{\parindent}{3.5\ccwd}},
}
\begin{document}
\begin{reidai}
求 $\dfrac{(1+i)^3(\sqrt{3}-1\i)}{1+\sqrt{3}i}$,文字测试内容文字测试内容 $1+\sqrt{3}i$,文字测试内容文字测试内容 $1+\sqrt{3}i$,文字测试内容文字测试内容 $1+\sqrt{3}i$,
\tcblower 因为文字测试内容文字测试内容 $1+\sqrt{3}i$,文字测试内容文字测试内容 $1+\sqrt{3}i$,文字测试内容文字测试内容 $1+\sqrt{3}i$,
\[
1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)
\]
\[
\sqrt{3}-i=2\left(\cos\left(-\frac{\pi}{6}\right)+i\sin \left(-\frac{\pi}{6}\right)\right)
\]
\[
1+\sqrt{3}i=2\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)
\]
所以 文字测试内容文字测试内容 $1+\sqrt{3}i$,文字测试内容文字测试内容 $1+\sqrt{3}i$,文字测试内容文字测试内容 $1+\sqrt{3}i$,文字测试内容文字测试内容 $1+\sqrt{3}i$,
$\begin{array}{l}
\text{原式}=\frac{(\sqrt{2})^3\times 2}{2}\left[\cos\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)+i\sin\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)\right] \\
\hspace{0.85cm}=2\sqrt{2}(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4})\\
\hspace{0.85cm}=2+2i
\end{array}$
\end{reidai}
\begin{reidaiA}
求 $\dfrac{(1+i)^3(\sqrt{3}-1\i)}{1+\sqrt{3}i}$
\tcblower 因为
\[
1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)
\]
\[
\sqrt{3}-i=2\left(\cos\left(-\frac{\pi}{6}\right)+i\sin \left(-\frac{\pi}{6}\right)\right)
\]
\[
1+\sqrt{3}i=2\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)
\]
所以
$\begin{array}{l}
\text{原式}=\frac{(\sqrt{2})^3\times 2}{2}\left[\cos\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)+i\sin\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)\right] \\
\hspace{0.85cm}=2\sqrt{2}(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4})\\
\hspace{0.85cm}=2+2i
\end{array}$
\end{reidaiA}
\begin{reidaiB}
求 $\dfrac{(1+i)^3(\sqrt{3}-1\i)}{1+\sqrt{3}i}$
\tcblower 因为
\[
1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)
\]
\[
\sqrt{3}-i=2\left(\cos\left(-\frac{\pi}{6}\right)+i\sin \left(-\frac{\pi}{6}\right)\right)
\]
\[
1+\sqrt{3}i=2\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)
\]
所以
$\begin{array}{l}
\text{原式}=\frac{(\sqrt{2})^3\times 2}{2}\left[\cos\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)+i\sin\left(\frac{\pi}{4}\times 3-\frac{\pi}{6}-
\frac{\pi}{3}\right)\right] \\
\hspace{0.85cm}=2\sqrt{2}(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4})\\
\hspace{0.85cm}=2+2i
\end{array}$
\end{reidaiB}
\end{document} 

这是从一个站点挪来的代码,效果如下;
\documentclass{ctexart}
\usepackage{tcolorbox}
\tcbuselibrary{breakable,theorems,skins}
%\tcbuselibrary{breakable} %%を読み込んでいます。
\newcounter{reidaibangou} %%カウンタの定義
\newtcolorbox{reidai}[1][]{enhanced,boxrule=0.5mm,
top=2pt,left=44pt,right=4pt,bottom=2pt,arc=0mm,
colframe=blue!30!gray,
boxrule=1pt,
underlay={
\node[inner sep=1pt,blue!50!black,fill=blue!10!white]at ([xshift=22pt,yshift=-9pt]interior.north west) {\stepcounter{reidaibangou}\bfseries\sffamily 例題\thereidaibangou};},
segmentation code={%
\draw[dashed] (segmentation.west)--(segmentation.east);
\node[inner sep=1pt,blue!50!black,fill=blue!10!white] at ([xshift=22pt,yshift=-8pt]segmentation.south west) {\bfseries\sffamily 解};},
before upper={\setlength{\parindent}{1\ccwd}},
before lower={\setlength{\parindent}{1\ccwd}},
}
%%%%%ここまでがreidai環境の定義。例えば本文中に以下のように記述してみよう。
\begin{document}
\begin{reidai}
次の問題に答えなさい。
\begin{enumerate}
\item 8人を2つの組に分ける方法は何通りあるか。
\item 6人を3つの部屋A,B,Cに入れる方法は何通りあるか。 {ただし}各部屋に少なくとも1人は入るものとする。
\end{enumerate}
\tcblower
区別があるかどうかを正しく考えます。
\begin{enumerate}
\item なんだかんだで127通り
\item なんだかんだで540通り
\end{enumerate}
\end{reidai}
\end{document}地址:https://marukunalufd0123.hatenablog.com/entry/2019/03/15/071717
有点瑕疵,“例2”这两个字没有与正文基线对齐,我就是在这个地方不能突破
\node[inner sep=1pt,white,fill=Back]at ([xshift=26pt,yshift=-8pt]interior.north west) {\stepcounter{reidaibangou}\sffamily 例~\thereidaibangou};这个里面的:“[xshift=26pt,yshift=-8pt]”改一下
@u7926 仅仅这样修改是不行的,要让它们自动实现基线对齐
这个盒子定义的文字以及其他装饰是置于正文文字的底层内容,把底层的内容固定好,正文内容作为一个填充也可使实现同样的效果吧,还是说您说的自动对齐不是我理解的意思!