如何消除Z方向的子向量绘制误差?
发布于 2024-04-05 16:42:38
按老师的指点,能绘制出已知曲面上点的法向量。我尝试再添加绘制已知点的X,Y,Z三个子向量时,出现Z子向量的误差,如何避免呢?请老师有空再分析看看,感激不尽。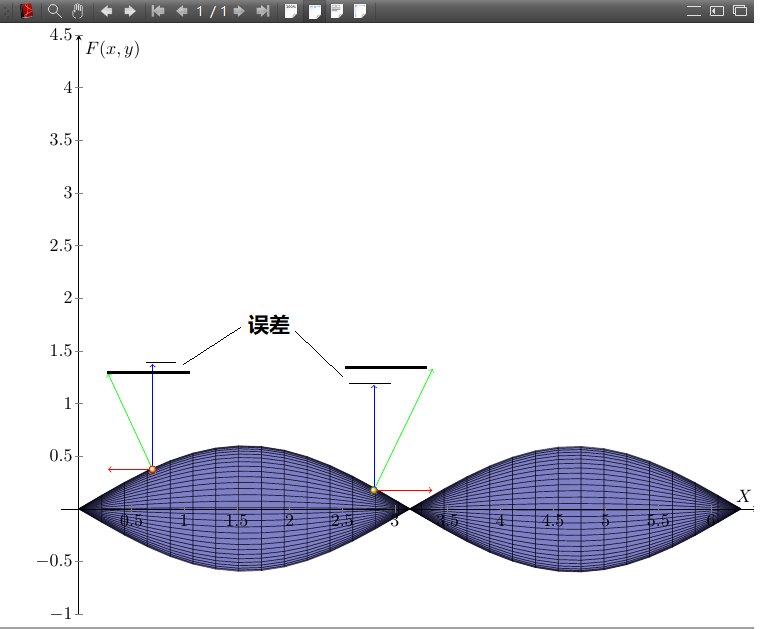
\documentclass[svgnames]{standalone}
\usepackage{tikz}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\begin{document}
\makeatletter
\newcommand\computegrad[4][0.00025]{% [delta], function, x, y
\begingroup\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\def\@tempdelta{#1}%
\pgfmathparse{#2(#3,#4)}\let\@tempz\pgfmathresult
\pgfmathparse{#2(#3+\@tempdelta,#4)}\let\@temppxa\pgfmathresult
\pgfmathparse{#2(#3-\@tempdelta,#4)}\let\@temppxb\pgfmathresult
\edef\@temppx{\fpeval{(\@temppxa-\@temppxb)/(2*\@tempdelta)}}%
\pgfmathparse{#2(#3,#4+\@tempdelta)}\let\@temppya\pgfmathresult
\pgfmathparse{#2(#3,#4-\@tempdelta)}\let\@temppyb\pgfmathresult
\edef\@temppy{\fpeval{(\@temppya-\@temppyb)/(2*\@tempdelta)}}%
\edef\@tempu{\fpeval{(\@temppx,\@temppy,-1)/sqrt(\@temppx^2+\@temppy^2+1)}}%
\edef\?{\endgroup\def\noexpand\pgfmathresult{\@tempu}%
\def\noexpand\pgfmathresulta{\fpeval{1*(#3,#4,\@tempz)-\@tempu}}}%
\?}
%%%%%%%%%%%%%%%%%green
\newcommand\computegraf[4][0.00025]{% [delta], function, x, y
\begingroup\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\def\@tempdelta{#1}%
\pgfmathparse{#2(#3,#4)}\let\@tempz\pgfmathresult
\pgfmathparse{#2(#3+\@tempdelta,#4)}\let\@temppxa\pgfmathresult
\pgfmathparse{#2(#3-\@tempdelta,#4)}\let\@temppxb\pgfmathresult
\edef\@temppx{\fpeval{(\@temppxa-\@temppxb)/(2*\@tempdelta)}}%
\pgfmathparse{#2(#3,#4+\@tempdelta)}\let\@temppya\pgfmathresult
\pgfmathparse{#2(#3,#4-\@tempdelta)}\let\@temppyb\pgfmathresult
\edef\@temppy{\fpeval{(\@temppya-\@temppyb)/(2*\@tempdelta)}}%
\edef\@tempu{\fpeval{(\@temppx,\@temppy,-1)/sqrt(\@temppx^2+\@temppy^2+1)}}%
\edef\?{\endgroup\def\noexpand\pgfmathresult{\@tempu}%
\def\noexpand\pgfmathresulta{\fpeval{1*(#3,#4,\@tempz)-\@tempu}}}%
\?}
%%%%%%%%%%%%%%%%%yellow
\newcommand\computegrag[4][0.00025]{% [delta], function, x, y
\begingroup\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\def\@tempdelta{#1}%
\pgfmathparse{#2(#3,#4)}\let\@tempz\pgfmathresult
\pgfmathparse{#2(#3+0,#4)}\let\@temppxa\pgfmathresult
\pgfmathparse{#2(#3-0,#4)}\let\@temppxb\pgfmathresult
\edef\@temppx{\fpeval{(\@temppxa-\@temppxb)/(2*\@tempdelta)}}%
\pgfmathparse{#2(#3,#4+\@tempdelta)}\let\@temppya\pgfmathresult
\pgfmathparse{#2(#3,#4-\@tempdelta)}\let\@temppyb\pgfmathresult
\edef\@temppy{\fpeval{(\@temppya-\@temppyb)/(2*\@tempdelta)}}%
\edef\@tempu{\fpeval{(\@temppx,\@temppy,0)/sqrt(\@temppx^2+\@temppy^2+1)}}%
\edef\?{\endgroup\def\noexpand\pgfmathresult{\@tempu}%
\def\noexpand\pgfmathresulta{\fpeval{1*(#3,#4,1*\@tempz)-\@tempu}}}%
\?}
%%%%%%%%%%%%%%%%%red
\newcommand\computegrah[4][0.00025]{% [delta], function, x, y
\begingroup\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\def\@tempdelta{#1}%
\pgfmathparse{#2(#3,#4)}\let\@tempz\pgfmathresult
\pgfmathparse{#2(#3+\@tempdelta,#4)}\let\@temppxa\pgfmathresult
\pgfmathparse{#2(#3-\@tempdelta,#4)}\let\@temppxb\pgfmathresult
\edef\@temppx{\fpeval{(\@temppxa-\@temppxb)/(2*\@tempdelta)}}%
\pgfmathparse{#2(#3,#4+0)}\let\@temppya\pgfmathresult
\pgfmathparse{#2(#3,#4-0)}\let\@temppyb\pgfmathresult
\edef\@temppy{\fpeval{(\@temppya-\@temppyb)/(2*\@tempdelta)}}%
\edef\@tempu{\fpeval{(\@temppx,\@temppy,0)/sqrt(\@temppx^2+\@temppy^2+1)}}%
\edef\?{\endgroup\def\noexpand\pgfmathresult{\@tempu}%
\def\noexpand\pgfmathresulta{\fpeval{1*(#3,#4,\@tempz)-\@tempu}}}%
\?}
%%%%%%%%%%%%%%%%%blue
\newcommand\computegral[4][0.00025]{% [delta], function, x, y
\begingroup\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\def\@tempdelta{#1}%
\pgfmathparse{#2(#3,#4)}\let\@tempz\pgfmathresult
\pgfmathparse{#2(#3+0,#4)}\let\@temppxa\pgfmathresult
\pgfmathparse{#2(#3-0,#4)}\let\@temppxb\pgfmathresult
\edef\@temppx{\fpeval{(\@temppxa-\@temppxb)/(2*\@tempdelta)}}%
\pgfmathparse{#2(#3,#4+0)}\let\@temppya\pgfmathresult
\pgfmathparse{#2(#3,#4-0)}\let\@temppyb\pgfmathresult
\edef\@temppy{\fpeval{(\@temppya-\@temppyb)/(2*\@tempdelta)}}%
\edef\@tempu{\fpeval{(\@temppx,\@temppy,-1)/sqrt(\@temppx^2+\@temppy^2+1)}}%
\edef\?{\endgroup\def\noexpand\pgfmathresult{\@tempu}%
\def\noexpand\pgfmathresulta{\fpeval{1*(#3,#4,\@tempz)-\@tempu}}}%
\?}
\makeatother
\begin{tikzpicture}
[declare function={f(\x,\y)=0.6*sin(deg(\x))*cos(deg(\y);}]
\begin{axis}[scale=2,axis equal,view={0}{0},axis lines=center,axis on top,zmax=4.5,zmin=-1,samples=30,xlabel={$X$},ylabel={$Y$},zlabel={$F(x,y)$}]%ticks=none,
\addplot3[surf,color=DarkBlue,opacity=0.5,domain=0:2*pi, y domain=0:3,faceted color=black] {f(x,y)};
%%define P
\addplot3+ [mark=ball,mark size=2pt,scatter src=rand,ball color=yellow!80!black!60]
coordinates {({0.7},{0.25},{f(x,y)})};
\addplot3+ [mark=ball,mark size=2pt,scatter src=rand,ball color=yellow!80!black!60]
coordinates {({2.8},{0.5},{f(x,y)})};
%space vector
\draw[->,green,shorten <=0cm]({0.7},{0.25},{f(0.7,0.25)})\pgfextra{\computegraf{f}{0.7}{0.25}} --\pgfmathresulta;
%y vector
\draw[->,yellow,shorten <=0cm]({0.7},{0.25},{f(0.7,0.25)})\pgfextra{\computegrag{f}{0.7}{0.25}} --\pgfmathresulta;
%x vector
\draw[->,red,shorten <=0cm]({0.7},{0.25},{f(0.7,0.25)})\pgfextra{\computegrah{f}{0.7}{0.25}} --\pgfmathresulta;
%z vector
\draw[->,blue,shorten <=0cm]({0.7},{0.25},{f(0.7,0.25)})\pgfextra{\computegral{f}{0.7}{0.25}} --\pgfmathresulta;
%%%
%space vector
\draw[->,green,shorten <=0cm]({2.8},{0.5},{f(2.8,0.5)})\pgfextra{\computegraf{f}{2.8}{0.5}} --\pgfmathresulta;
%y vector
\draw[->,yellow,shorten <=0cm]({2.8},{0.5},{f(2.8,0.5)})\pgfextra{\computegrag{f}{2.8}{0.5}} --\pgfmathresulta;
%x vector
\draw[->,red,shorten <=0cm]({2.8},{0.5},{f(2.8,0.5)})\pgfextra{\computegrah{f}{2.8}{0.5}} --\pgfmathresulta;
%z vector
\draw[->,blue,shorten <=0cm]({2.8},{0.5},{f(2.8,0.5)})\pgfextra{\computegral{f}{2.8}{0.5}} --\pgfmathresulta;
\end{axis}
\end{tikzpicture}
\end{document}关注者
0
被浏览
1.4k

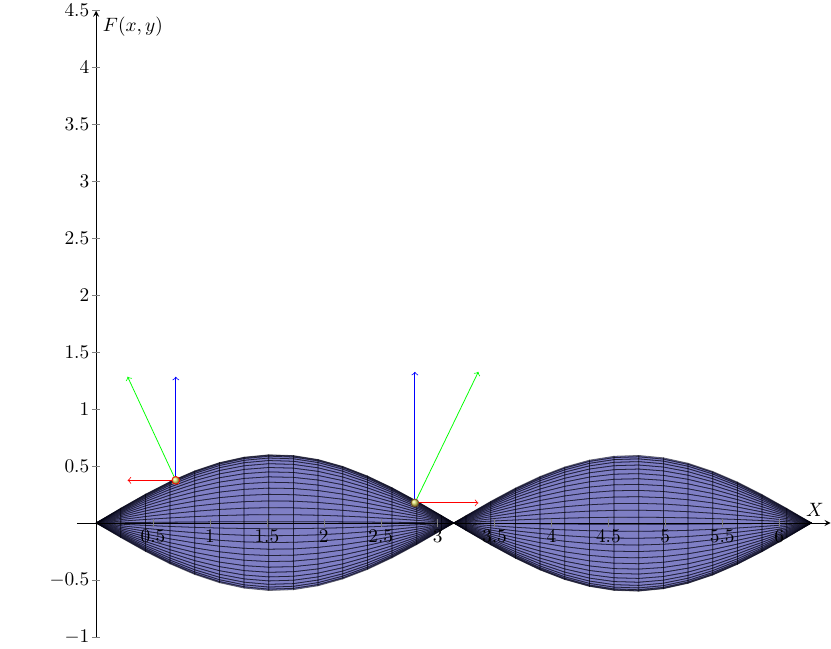





谢谢老师的完美指导。
为了突出已知点上法向量的空间构造,我又补了几条虚线,但是都靠肉眼绘制,如果已知点坐标变化了,就不能实现了。老师您有空在帮我看看,谢谢。
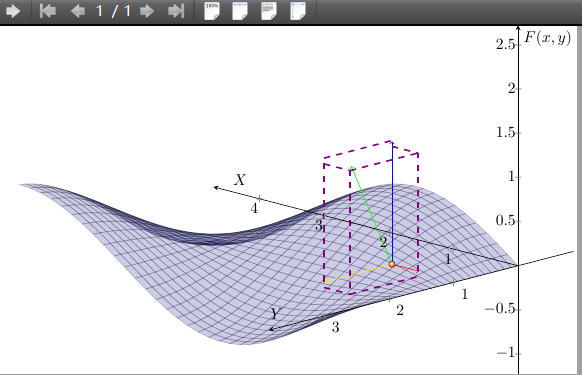
@U7117 在
\computegrad/h/..计算完成之后,把结果保存下来,然后用向量计算公式计算端点的坐标。\fpeval可以直接计算向量的和。@u10307 老师,我还是没掌握这种方法,不知代码如何写。要不您有时间再指点一下我。
@U7117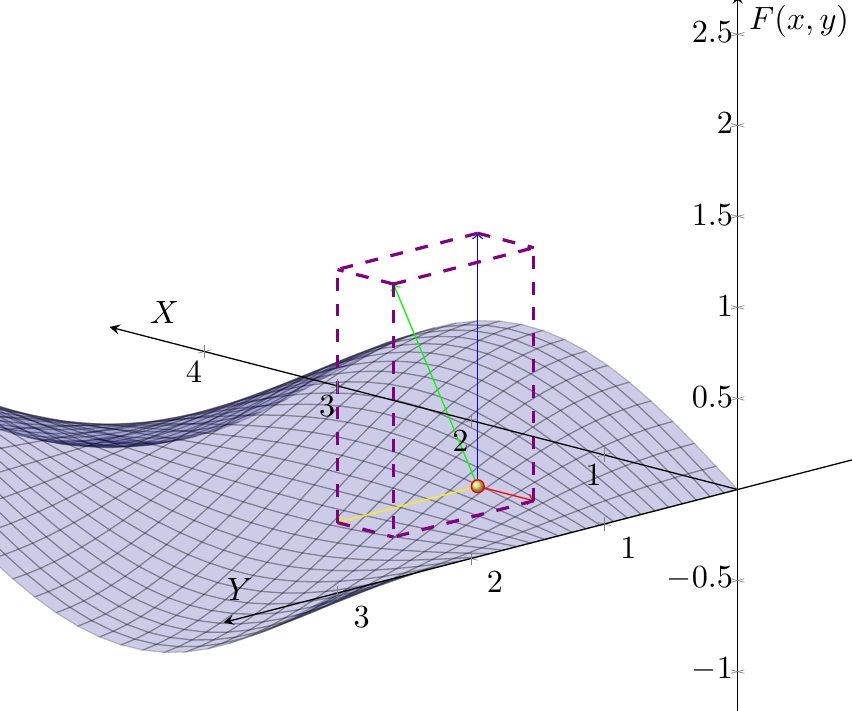
@u10307 完美解决,很感激老师。