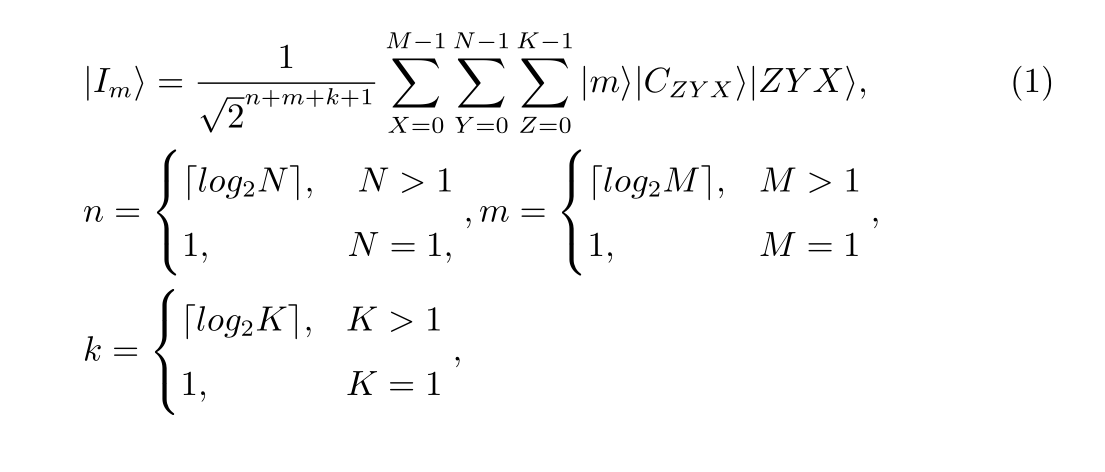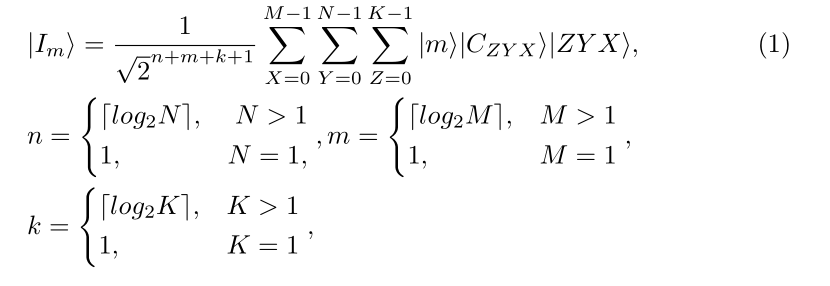想问一下,我这个竖线|为啥latex识别不了呢,别人的好像就可以 ,总报错,我确定是这行公式错了,用的TexSudio和pdfLatex
发布于 2021-12-19 14:53:25

\begin{align}
%&$\mid$$I_m$$\rangle$=$\frac{1}$${\sqrt{2}^{n+m+k+1}}$$\sum_{X=0}^{M-1}{}$$\sum_{Y=0}^{N-1}{}$$\sum_{Z=0}^{K-1}{$\mid$$m$$\rangle$$\mid$$C_{ZYX}$$\rangle$$\mid$$ZYX$$\rangle$}$, \label{eq:1}\\
&|I_{m}\rangle = \frac{1}{\sqrt{2}^{n+m+k+1}}\sum^{M-1}_{X=0}\sum^{N-1}_{Y=0}\sum^{K-1}_{Z=0}|m\rangle|C_{ZYX}\rangle|ZYX\rangle, \label{eq:1}\\
&n=\left\{
\begin{aligned}
&\lceil log_2N\rceil, &N>1 \\
&1,&N=1,
\end{aligned}
\right.,
m=\left\{
\begin{aligned}
&\lceil log_2M\rceil, &M>1 \\
&1,&M=1
\end{aligned}
\right., \nonumber \\
&k=\left\{
\begin{aligned}
&\lceil log_2K\rceil, &K>1 \\
&1,&K=1
\end{aligned}
\right., \nonumber
\end{align}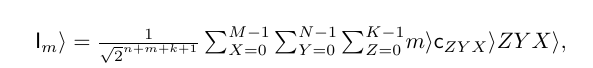
关注者
0
被浏览
5.1k