可以使用tkz-euclide和tkz-elements这两个欧氏几何绘图宏包来画。
需要使用lualatex来编译。
\documentclass[tikz,border=2pt]{standalone}
\usepackage{tkz-euclide,tkz-elements}
\begin{document}
\begin{tkzelements}
z.O = point: new (0 , 0)
z.x1 = point: new (1 , 0)
z.A = point: new (2 , 0)
z.B = point: new (0 , 1)
E= ellipse: new (z.O,z.A,z.B)
ang = math.deg(E.slope)
z.P = point: new (1 , 2)
L.T1,L.T2= E : tangent_from (z.P)
z.T1 = L.T1.pb
z.T2 = L.T2.pb
L.x = line : new (z.O ,z.x1)
z.C= intersection (L.T1,L.x)
z.D= intersection (L.T2,L.x)
\end{tkzelements}
\begin{tikzpicture}
\draw [gray!70] (-4,-4) grid (4,4);
\draw [->] (-4,0) -- (4,0) node [below left] {$x$};
\draw [->] (0,-4) -- (0,4) node [below left] {$y$};
\tkzGetNodes
\tkzDrawEllipse(O,\tkzUseLua{E.Rx},\tkzUseLua{E.Ry},\tkzUseLua{ang})
\tkzDrawSegments(P,C P,D)
\tkzDrawPoints(P,T1,T2,C,D)
\tkzLabelPoints[above](P,T1)
\tkzLabelPoints[below](C,D)
\tkzLabelPoints[right](T2)
\tkzLabelPoints[below left](O)
\end{tikzpicture}
\end{document} 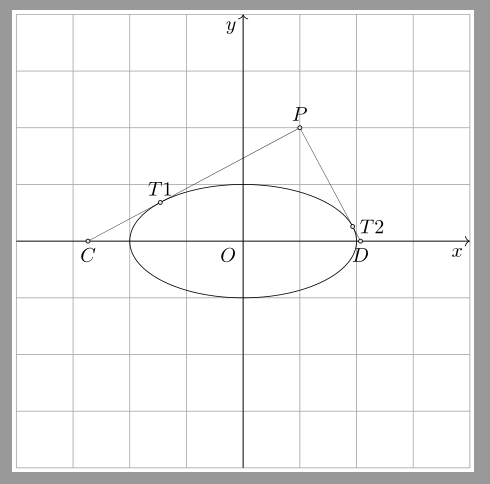
4 个回答
我是不懂这个代码的,both 数学原理 and LaTeX Tikz实现
我只是个轮子的搬运工
参考(copy)自下面的链接John Kormylo‘s brilliant solution on TSE
\documentclass[tikz,border=2pt]{standalone}
\usetikzlibrary{calc,intersections}
\newlength{\bigenough}
\newcount\total
% locates both points on a closed shape tangent to a point outside the shape.
% \tangent{pathname}{center}{point}{first}{second}
\newcommand{\tangent}[5]% #1=path name for shape, #2=coordinate name for center, #3=cordinate name for outside point
{\begingroup% #4=coordinate name for first tangent point, #5=coordinate name for second coordinate point
\setlength{\bigenough}{1cm}
\loop% loop until big enough
\path[name path=temp] ($(#2)!\bigenough!-90:(#3)$)--($(#2)!\bigenough!90:(#3)$);
\path[name intersections={of = #1 and temp, total=\t}]%
\pgfextra{\global\total=\t};%
\ifnum\total<2 \global\bigenough=2\bigenough\repeat%
\endgroup
\coordinate (#4) at (intersection-1);% initial guess
\coordinate (#5) at (intersection-2);%
\tangentsearch{#1}{#2}{#3}{#4}%
\tangentsearch{#1}{#2}{#3}{#5}}
% find tangent using binary search
\newcommand{\tangentsearch}[4]% #1=path name for shape, #2=coordinate name for center, #3=cordinate name for outside point
{\begingroup% #4=coordinate name for tangent point (initail guess -> final)
\loop% loop until only 1 intersection
\path[name path=temp] (#3)--($(#4)!-\bigenough!(#3)$);
\path[name intersections={of = #1 and temp, total=\t}]%
\pgfextra{\global\total=\t};%
\ifnum\total=2 \coordinate (#4) at ($(intersection-1)!0.5!(intersection-2)$);
%\draw[pink] (intersection-1)--(intersection-2);% included only for debugging purposes
\path[name path=temp] (#4)--($(#4)!-\bigenough!(#2)$);
\path[name intersections={of = #1 and temp}];%
\coordinate (#4) at (intersection-1);%
\repeat%
\endgroup}
\begin{document}
\begin{tikzpicture}
\draw [gray!70] (-4,-4) grid (4,4);
\draw [->] (-4,0) -- (4,0) node [below left] {$x$};
\draw [->] (0,-4) -- (0,4) node [below left] {$y$};
\draw[name path=ellipse,thick,fill=gray!30,opacity=0.5] (0,0) ellipse (2 and 1);
% \draw [thick] (2,0) arc (0:360:2 and 1);
%\coordinate (O) at (0,0);
%\node at (O) [below left] {$O$};
%这里可以缩行
\coordinate[label={below left:$O$}] (O);
% \coordinate (P) at (1,2);
% \fill (P) at (1,2) circle (1pt) node [above right] {$P$};
%这里也可以缩行
\node[label={above right:$P$},circle, fill, inner sep=1pt] (P) at (1,2) {};
\tangent{ellipse}{O}{P}{X}{Y}
\draw (X)--(P)--(Y);
\end{tikzpicture}
\end{document}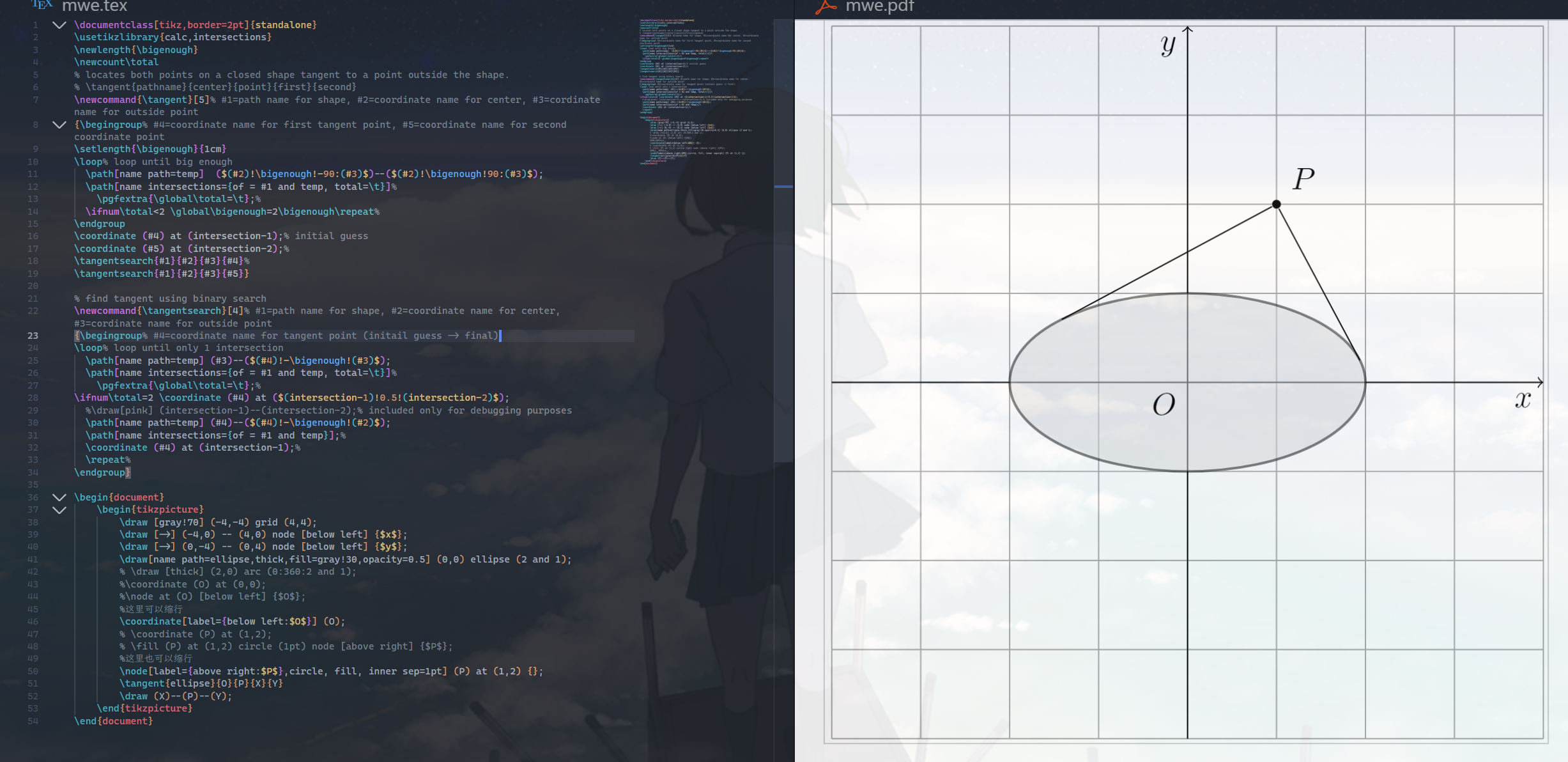
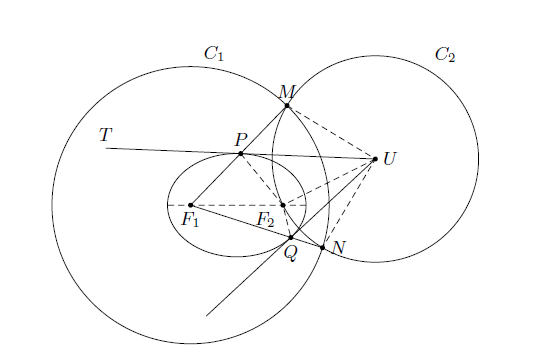
感谢群友@香港-小狮子提出了一种较为简单的几何画法!其余参与讨论的大家,一并感谢您们的指导!
方法肯定不止这一种,后续我将继续整理讨论结果,同时十分欢迎提出新的回答!
\documentclass[tikz,border=2pt]{standalone}
\usetikzlibrary{calc,intersections}
\usepackage{amsmath}
\begin{document}
\begin{tikzpicture}[scale=2]
\draw [->] (-3,0) -- (3,0) node [below left] {$x$};
\draw [->] (0,-3) -- (0,3) node [below left] {$y$};
\draw [help lines] (-3,-3) grid (3,3);
\clip (-3.1,-3.1) rectangle (3.1,3.1);
\draw [thick] (2,0) arc (0:360:2 and 1) node at (-2,-2) {$\dfrac{x^2}{4}+y^2=1$};
\node (O) at (0,0) [below left] {$O$};
\fill (1,2) circle (1pt) coordinate (P) node [above right] {$P(1,2)$};
\fill ({-sqrt(3)*1cm},0cm) circle (1pt) coordinate (F1) node [below] {$F_1$};
\fill ({sqrt(3)*1cm},0cm) circle (1pt) coordinate (F2) node [below] {$F_2$};
\path let \p1=($(P)-(F2)$),\n1={veclen(\x1,\y1)}
in [dotted,name path=cirP] (P) circle (\n1);
\path [dotted,name path=cirF1] (F1) circle (4);
\path [name intersections={of=cirP and cirF1,by={J1,J2}},dashed] (J1)--(F2) (J2)--(F2);
\draw let \p1=(J1),\p2=(F2),\n1={\y2-\y1},\n2={\x2-\x1},\n3={atan{\n1/\n2}-90}
in [ultra thick,red] (P)--++(\n3:4cm);
\draw let \p1=(J2),\p2=(F2),\n1={\y2-\y1},\n2={\x2-\x1},\n3={atan{\n1/\n2}-90}
in [ultra thick,red] (P)--++(\n3:3cm);
\end{tikzpicture}
\end{document}撰写答案
请登录后再发布答案,点击登录









在学习
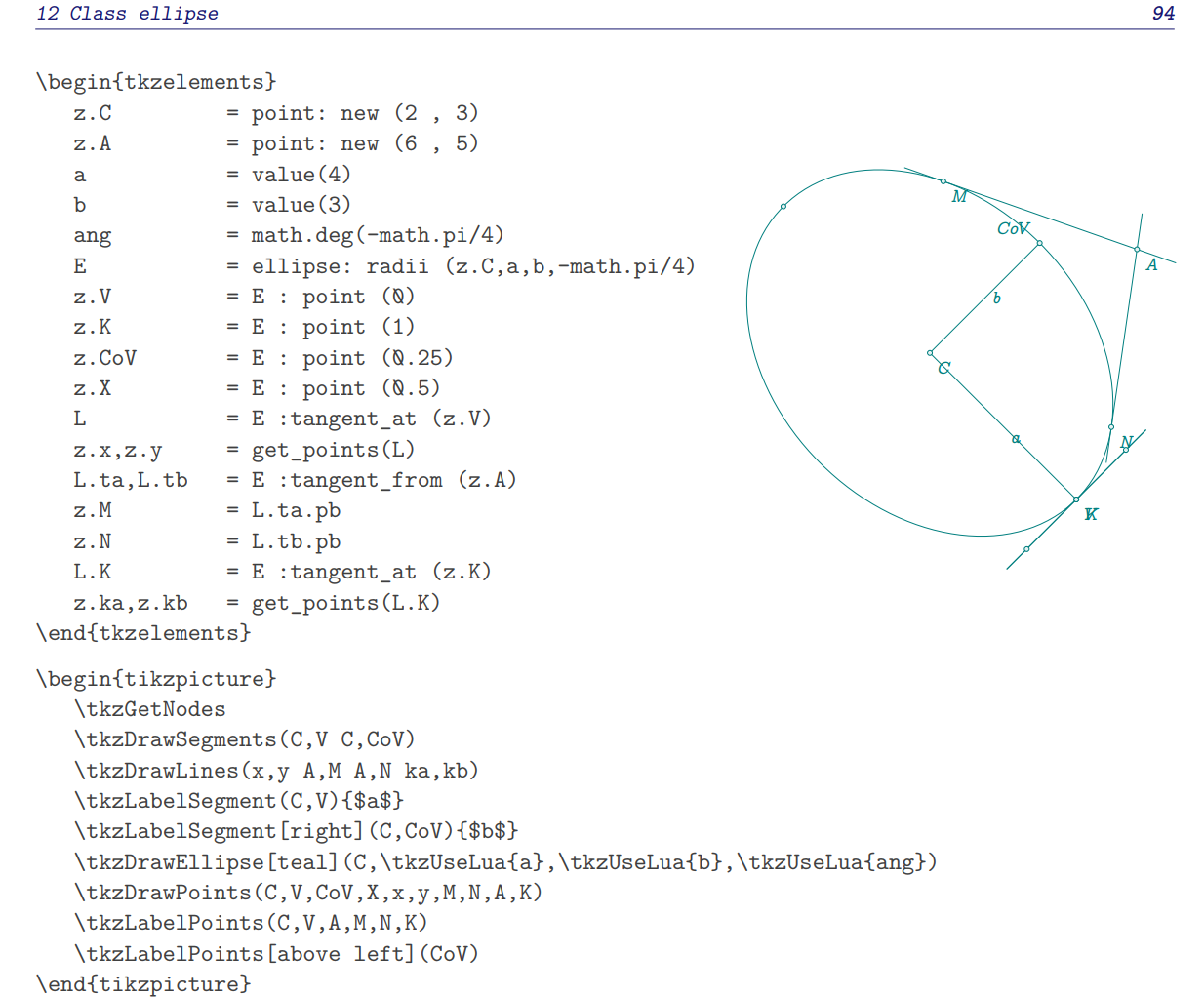
tkz-elements宏包,这一OOP的方法在文档中有直观的介绍:@u101077
update:2025-06
近期
tkz-elements的语法发生了「剧烈」的破坏性更新在「v4.15」的
tkz-elements,一份可行的代码为: