如果用 tikz 的话, 建议分段绘制.
f(x) = sqrt(16 / (x + 2)^2 - (x - 2)^2), -1 <= x <= 0,
g(x) = sqrt(16 / (x + 2)^2 - (x - 2)^2), 0 <= x <= 2.6,
h(x) = sqrt(16 / (x + 2)^2 - (x - 2)^2), 2.6 <= x <= 2*sqrt(2),这条曲线在 (0,0) 点处不光滑, 在 (2*sqrt(2),0) 处导数值无穷, 适合分段
\documentclass[tikz,border=5pt]{standalone}
\usepackage{xfp}
\begin{document}
\begin{tikzpicture}[line cap=round]
\draw[-stealth] (-1.5,0)--(3,0)node[scale=0.7,right]{$x$};
\draw[-stealth] (0,-3)--(0,3)node[scale=0.7,left]{$y$};
\node[label={[anchor=north east,yshift=-.1em]$o$}] {};
\def\sp{2.6}%第二, 三段的分点
\def\sampleNOa{10}\edef\stepa{\fpeval{1/\sampleNOa}}%第一段的点数量, 自变量步长
\def\sampleNOb{30}\edef\stepb{\fpeval{\sp/\sampleNOb}}%第二段的点数量, 自变量步长
\def\sampleNOc{60}\edef\stepc{\fpeval{(2*sqrt(2)-\sp)/\sampleNOc}}%第三段的点数量, 自变量步长
\foreach \z/\p in {a/-1,b/0,c/\sp}{
\expandafter\let\expandafter\sampleNO\csname sampleNO\z\endcsname
\expandafter\let\expandafter\step\csname step\z\endcsname
\edef\PL{\fpeval{\p,sqrt(16/(\p+2)^2-(\p-2)^2)}}
\foreach \i in {1,2,...,\sampleNO}{
\xdef\PL{\PL \fpeval{\p + \i*\step, sqrt(16 / (\p + \i*\step + 2)^2 - (\p + \i*\step - 2)^2)}}
}
\draw plot[smooth] coordinates {\PL};
}
\end{tikzpicture}
\end{document}
如果能求出 h(x) 的反函数, 或者曲线的参数表示, 需要绘制的点的数量还可能会更少.













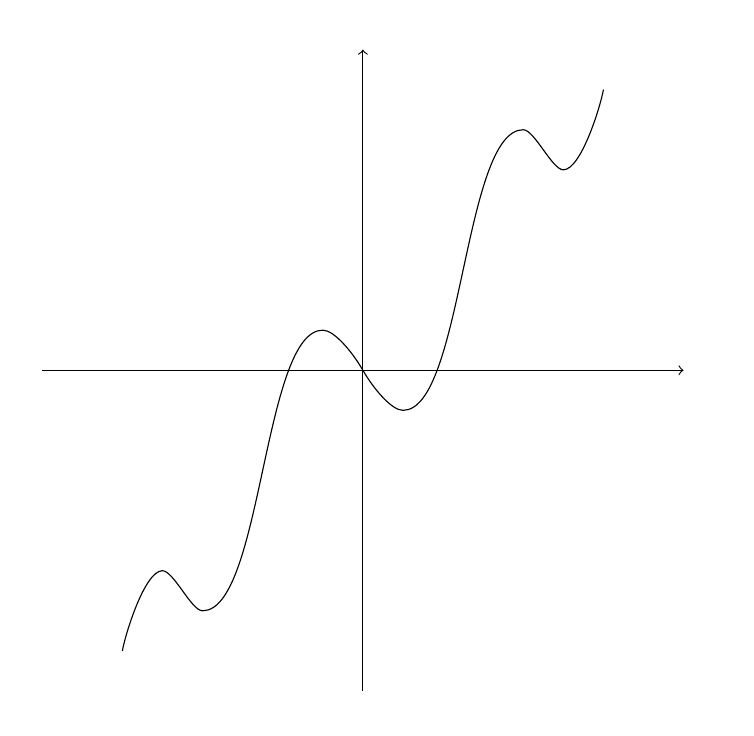

问 用`tikz`中的`polt`绘制`y=sqrt{16/(x+2)^2-(x-2)^2}`的图像时最右端部分无法闭合?