10 下图中B、C两个图象对应函数的解析式如何确定?谢谢
经常看到类似的已知图象,函数图象未知的情况,这类函数的解析式有什么一般思路知道或猜到吗?谢谢!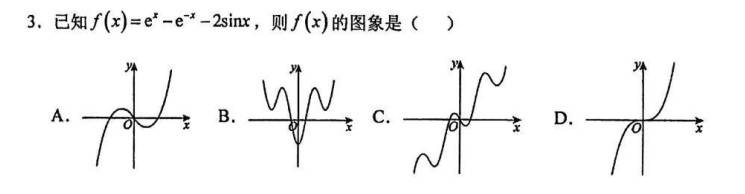
经常看到类似的已知图象,函数图象未知的情况,这类函数的解析式有什么一般思路知道或猜到吗?谢谢!
或者使用 tikz 的 to 路径.
%\usetikzlibrary{topaths}
\begin{tikzpicture}
\draw [->] (-4,0) -- (4,0);
\draw [->] (0,-4) -- (0,4);
\def\rightpart{
(0,0) to[out=-60,in=180,in looseness=0.5] (0.5,-0.5)
to[out=0,in=180,out looseness=0.5,in looseness=0.5] (2,3)
to[out=0,in=180,out looseness=0.5,in looseness=0.5] (2.5,2.5)
to[out=0,in=-100,out looseness=0.5,in looseness=0.5] (3,3.5)
}
\draw \rightpart ;
\draw[rotate=180]\rightpart ;
\end{tikzpicture}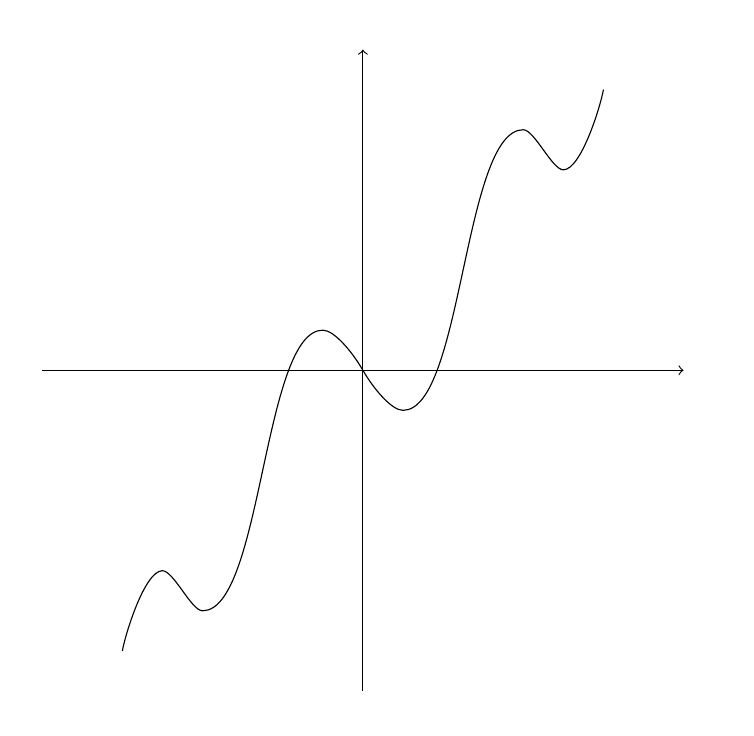
找点直接连吧,简单粗暴!
\begin{tikzpicture}
\tkzInit[xmin=-2,xmax=2,ymin=-2,ymax=2]
\tkzDrawX[black,thick,noticks , ]
\tkzDrawY[black,thick,noticks , ]
\node at (-0.2,-0.2){$O$};
\tkzDefPoints{-1.76/1.99/A,-1.33/0.52/B,-0.76/1.63/C,0/-1.18/D,0.82/1.63/E,1.39/0.49/F,1.84/1.97/G}
\draw[blue] plot[smooth,samples=500,tension=0.9] coordinates{(A)(B)(C)(D)(E)(F)(G)};
\end{tikzpicture}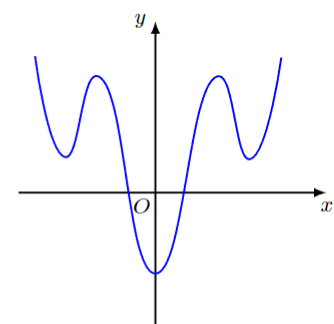
A:有两个极值点,三次函数应该可以。又因为三个零点:-1,0,1(-1,1也可以是-2,+2,可调):y=(x-0)(x-1)(x+1)=x(x^2-1).
B:有五个极值点,六次函数。图中有两个零点,但如果向下平移,可以有六个关于0对称的零点。y=(x^2-5)(x^2-4)(x^2-0.5)+2,其中5,4两个数近点,然后调节 0.5 的大小使图像接近,最后调节2,使零点只有两个。
C:是答案.但不做严格要求的话,可以看出,函数是振荡的,但整体是在增加。简单的话可以看成一个正比例函数与一个正弦函数的和或差:y=1x-3sinx,其中1,3可调;但图上振荡的幅度远离原点时变小了,所以可以把正比例函数换成的指数大于1的幂函数(须要保证是奇函数),但整数幂的话3又太大了,取用分数指数幂,这个最简分数的分子分母要是互质的奇数(保证奇函数所须),比如,11/9,13/9, 所以 y=1x^(11/9)-3sinx当然1,11/9,3是可以调的。
D:最简单的奇次幂函数就可以,比如3,5次等, y=x^3就可以。当然也可以像C选项一样改变指数为分数指数幂。
对这种简单情况, 用贝塞尔曲线拼接, 只需要选定几个特征点, 几乎就是瞪眼法. 操作过 inkscape 的钢笔工具的话, 还是比较容易的, 至少要比拼凑函数解析式容易.