20 规律图形怎样平移?基础图形已画
发布于 2024-11-27 12:55:13
关注者
0
被浏览
1.1k
我觉得平移很难操作,而且存在浮点计算误差....
另外scope环境是用于多个画面的,在你这个case下我个人觉得不太适合...
打小就不会找规律,提供一个我觉得非常丑陋的做法...
当然封装成函数便于复用同时加上scope这些得你自己来了,本问题的关键在于找到循环的pattern...
\documentclass[border=1.2cm]{standalone}
\usepackage{tkz-euclide}
\usetikzlibrary{calc}
\pgfmathtruncatemacro{\NN}{10}
\newcommand*{\stepfurther}[2]{
\ifodd#1
\tkzDefSquare(B#1,A#1)\tkzGetPoints{A#2}{C#2}
\tkzDrawPolygon[fill=gray!20](B#1,A#1,A#2,C#2)
\tkzDefTriangle[equilateral](C#2,A#2)\tkzGetPoint{B#2}
\tkzDrawPolygon(A#2,C#2,B#2)
\tkzDefTriangle[equilateral](B#1,C#2)\tkzGetPoint{E#2}
\tkzDrawPolygon(B#1,C#2,E#2)
\tkzDefTriangle[equilateral](A#2,A#1)\tkzGetPoint{D#2}
\tkzDrawPolygon(A#2,A#1,D#2)
\else
\tkzDefSquare(B#1,A#1)\tkzGetPoints{C#2}{B#2}
\tkzDrawPolygon[fill=gray!20](B#1,A#1,C#2,B#2)
\tkzDefTriangle[equilateral](B#1,B#2)\tkzGetPoint{D#2}
\tkzDrawPolygon(B#1,B#2,D#2)
\tkzDefTriangle[equilateral](C#2,A#1)\tkzGetPoint{E#2}
\tkzDrawPolygon(C#2,A#1,E#2)
\tkzDefTriangle[equilateral](B#2,C#2)\tkzGetPoint{A#2}
\tkzDrawPolygon(C#2,B#2,A#2)
\fi
% \node at (A#2) {$A_#2$};
% \node at (B#2) {$B_#2$};
}
\begin{document}
\begin{tikzpicture}
\tkzDefPoint(0,0){B0}
\tkzDefPoint(-120:1){A0}
\tkzDefPoint(-1,0){C0}
\tkzDrawPolygon(A0,B0,C0)
\foreach \i[count = \cnt from 0] in {1,...,\NN}{
\stepfurther{\cnt}{\i}
}
\end{tikzpicture}
\end{document}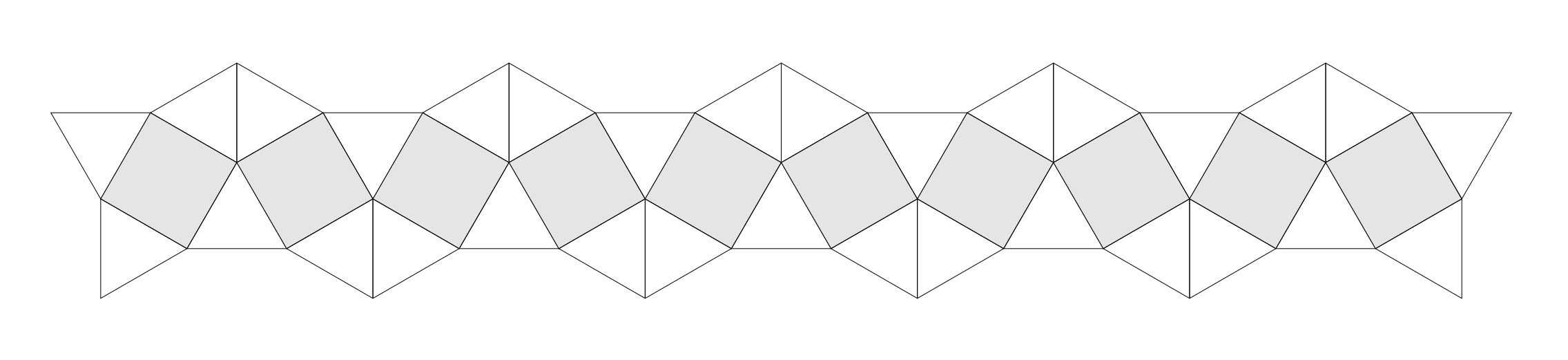
期待更优雅的做法~
BTW, 上面有两个方向的
stepfurther方式,不得已采用了顺次迭代+条件判断的方法...而且传参数的方式也不是很优雅....谢谢您!期待其它解法