圆柱表面绘制与渲染方法
发布于 2024-04-20 14:30:11
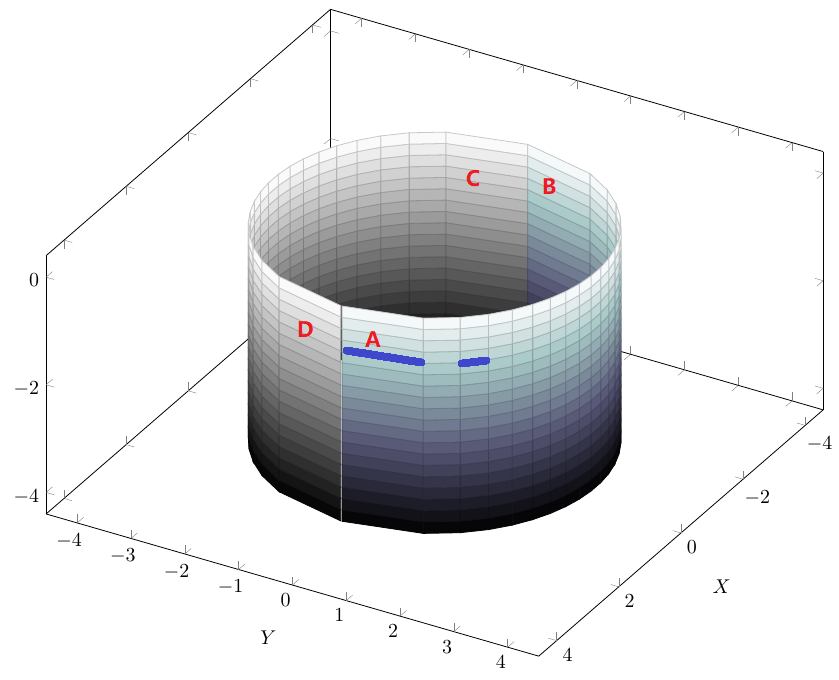
图中,使用使用自定义函数的方式绘制的圆柱曲面,有如下两个问题:
- 如何将两条绘制命令合并为一条命令?要求不使用参数方程,仍然使用自定义函数的方式
- 图中ABCD四个位置明显渲染效果面积比其它位置大,如果增加样本量,这个现象还是存在。如何做到绘出基本均匀的网格线?
\documentclass{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.18}
\usepgfplotslibrary{colormaps,fillbetween}
\begin{document}
\begin{tikzpicture}[declare function={f(\x)=sqrt(9-\x^2);}]
\begin{axis}[scale=2,axis equal,view={120}{30},samples=20,xlabel={$X$},ylabel={$Y$}]
\addplot3[colormap/blackwhite,surf,z buffer=sort,,domain=-3:3, y domain=-4:0] (x,{-1*f(x)},y);
\addplot3[colormap/bone,surf,z buffer=sort,,domain=-3:3, y domain=-4:0] (x,{f(x)},y);
\end{axis}
\end{tikzpicture}
\end{document}关注者
0
被浏览
2.7k







