一份勉强简短的 LaTeX3 编程介绍

原文地址：https://zhuanlan.zhihu.com/p/408331900

千呼万唤始出来，犹抱琵琶半遮面。

转轴拨弦三十年，未成L3先有expl3。

随着2020年新冠疫情的席卷全球，L3 programming layer 也就是宏包 expl3 终于修成了正果，正式被集成进了LaTeX内核，此后，无需 \usepackage{expl3} 便可直接使用L3语法了。

为了打字方便，使用缩写，LaTeX2e(L2e)，LaTeX3(L3)

继之前的文章说过，L2e的名字源于L3的发布遥遥无期。那自然遥遥无期，因为L3项目组放弃了将L3独立于L2e的想法，而是直接将其集成进L2e中，对LaTeX进行现代化改造，丰富和发展文学编程。

然而，国内目前关于L3编程的东西仍凤毛麟角寥若晨星。诸君莫辞更坐歇一会，为卿铺路L3编程。

关键字：LaTeX3，expl3宏包，LaTeX3教程

1 为什么要学LaTeX3，LaTeX2e又不是不能用！

这部分可以直接跳过

使用LaTeX而非Word的好处不再多说。然LaTeX也并非简单的排版语言，在大型文档生成过程中编程也是非常重要的。

1.1 L2e的编程接口混乱

不同的编程接口可能在不同的宏包，不同宏包可能具有高度相似的编程接口实现。？？？

1.2 L2e混淆的概念

L2e中变量和函数使用相同的命令（一般\newcommand 甚至原生\def）来定义，且命名也没有规范的方法

1.3 L2e迷人的宏展开控制

L2e归根结底是TeX写的，TeX终究是一个宏定义语言，有时不可避免地要控制宏展开的顺序。比如，如果要控制以下内容的宏展开顺序

逆序展开该内容，即使得展开顺序为DCBA，则需要如此控制

\expandafter\expandafter\expandafter
\expandafter\expandafter\expandafter
\expandafter A\expandafter\expandafter
\expandafter B\expandafter CD

这代码可不是用来吓人的（的确是），可以用人脑模拟展开一下，最终的展开顺序的确是DCBA。本想多举几个例子，但由于该部分并不重要，便不过多阐述。我总结了两条使用\expandafter宏展开控制的规律

• 如果Token1需要其后面n个token在其之前展开，着则需要在其之前加​ 2n−12^n-1个 \expandafter。
• 如果n个Token需要逆序展开，则需要​ 2n−n−12^n-n-1 个\expandafter

有同学会问什么叫"有时不可避免地要控制宏展开的顺序"，比如如下代码：

\def\contents{contents}
\uppercase{prefix\contents}

很简单的两行，看看结果是否如愿。而正确的写法为：

\expandafter\uppercase\expandafter{\expandafter p\expandafter r\expandafter e\expandafter f\expandafter i\expandafter x\contents}

2 拥抱LaTeX3

LaTeX2e的编程接口已经图灵完备，而LaTeX3接口旨在提供具有现代高级语言（如C++，Python）的特性。

系统地学习一门编程语言的途径永远都是官方文档。而个人认为一份通俗易懂的教程的意义在于破除自身与过于复杂的官方文档的之间的壁垒。本文章亦是如此，不会系统介绍L3编程接口，但会提供解决一个实际问题的大部分编程知识。

LaTeX3接口旨在提供具有现代高级语言的特性，那么本文章的内容也基于一般高级语言学习的流程而展开，并尽可能忽略掉非高级语言没有的特性。可是呀，TeX终究还是宏定义语言，终究还是要先从控制序列(Control Sequence，cs)开始讲起。在L3中，控制序列你可以认为就是函数了。

2.1 LaTeX3编程环境

如何安装一个LaTeX发行版？本文自然是不会涉及到了。这里主要是介绍下如何开启L3的编程环境接口。即使expl3 已经加入LaTeX内核，但使用L3的编程环境还是需要通过两个宏命令\ExplSyntaxOn和\ExplSyntaxOff来开启和关闭，因为L3中的函数和变量命名加入了:和_，需要通过这两个命令调整这两个符号的类别码 Category Code，前者将这两个符号的类别码设为11（代表着字母），而后者恢复它们原来的类别码。这犹如在L2中我们常常成对使用\makeatletter和makeatother调整@的类别一样。因此，开启L3编程环境很简单，只需要将代码包在两个宏定义之间即可。

\ExplSyntaxOn

% Your LaTeX3 code

\ExplSyntaxOff

那么问题来，将:和_设为字母类别后，在其它模式下我们需要这些符号表达特定含义时怎么办，目前以我的经验是使用\c_colon_str代替冒号和使用\c_math_subscript_token代替下划线。还有就是，在该模式中所有的空格和换行都会被忽略，可以使用~和\来代替空格。

2.2 函数有了参数申明

一个完整的函数名称由名字<module>_<description>和参数说明符组成<arg-spec>，并使用冒号隔开。

\<module>_<description>:<arg-spec>

函数名字<module>_<description>一般反应了其所属模块和该函数的说明，由下划线隔开，L3自带的函数都是这种形式。这只是一种命名规范，你不遵守也没问题，编译也能通过，因为后面等你命名不规范而导致代码混乱时，才会发现有大问题。建议养成良好的命名习惯，不过如果是初学，那也就没必要刻意强制自己了，在比较短的玩具代码中，简单的命名反而更好观察。

函数最重要的部分便是参数说明符<arg-spec>了。参数说明符一般为单个字符，申明函数的参数类型，可以理解为C++函数的形参类型申明或Python函数中的参数标注。实际上更加偏向前者，因为参数说明符在L3中是有意义的，控制着函数如何“吃”参数，而python标注只是给开发者和IDE看，解释器并不做任何处理。下面列举几个常用的参数说明符：

N & n： 原模原样地接收一个token，不过 N 一般接收单个token，通常用来接收控制序列，而 n 接收由花括号括起来的所有token

T & F： 一般用于条件分支语句中，接收条件分支语句相应true和false的代码

p： 用于接收TeX形式的参数文本，如#1#2#3这种东西

w： 所谓"魔法参数说明符"，接收在终止符(\q_stop)之前出现的所有内容

L3终究还是宏定义语言，那也就是我们定义函数的工具也是函数。回想一下TeX中定义一个控制序列的方法：

\def\cmd#1#2{\uppercase{#1,#2}}

那么思考L3中的\def应该长什么样。可以看出，\def的参数可以分为三个部分，\cmd，#1#2和\uppercase{#1,#2}。从上面的介绍可知，在L3中接收这三种文本的参数说明符分别为N，p和n。因此可以推理出，L3中定义函数的命令名称应该是这种形式：

\xxx_xxx:Npn   % 对应Python里面的def

同理我们可以猜出声明变量，赋值变量等等的命令形式：

\xxx_xxx:N     % 申明变量的命令，对应C++里的 int，float，char
\xxx_xxx:Nn    % 定义变量的命令，可以认为是 set(variable,value)

至此，正式开始L3编程的学习

2.3 数据类型

在L3中变量拥有了命名规范：

\<scope>_<module>_<description>_<type>

在L3中还引入了高级语言中的私有(private)变量和函数概念，私有变量和函数的命名很简单，类似Python语言的私有变量，在模块名<module>前面加下划线即可。

\<scope>__<module>_<description>_<type>    % 私有变量
\__<module>_<description>:<arg-spec>       % 私有函数

这种规范的命名可以很清晰地从名字看出一个变量的作用域和类型。

变量的作用域分为三种：

• l: 局部(local)变量
• g: 全局(global)变量
• c: 全局常数(constant)

变量作用域这东西，有编程基础的都懂，不懂那也不必在学一个宏定义语言的初级阶段学作用域是什么，徒增入门的困难程度，可以直接跳过。不过值得注意的是，C++使用花括号，Python使用缩进控制作用域，而L3中使用一对\group_begin:和\group_end:来控制作用域

\group_begin:
  % 局部作用域
\group_end:

记得命令末尾的冒号，在L3规范中，即使函数没有参数，也应该有个冒号

变量的类型有很多，有基础数据类型，也有高级数据结构，本着简洁的原则，本文

主要介绍整数(int)，浮点数(fp)，字符串(str)和序列(seq)。

正如上一节推测的一般，控制变量的命令以N或Nn结尾，可以分为三种类型：

• <type>_new:N 申明一个类型为<type>的变量，如果已经声明则会报错
• <type>_set:Nn 为一个已经声明的变量赋值
• <type>_gset:Nn 为一个已经声明的变量赋值，全局可见

<type>_set:Nn和<type>_gset:Nn 都是修改变量，区别是一个是局部修改，一个是全局修改。本文后续大都使用<type>_set:Nn。

2.31 整数（Integer, int）

定义一个变量名\l_my_lipsum_int为整数，与其同质的C++和Python代码也在注释里给出：

\int_new:N \l_my_lipsum_int

% C++:
% int l_my_lipsum_int;
%
% Python:
% l_my_lipsum_int:int = 0

将其值设为6：

\int_set:Nn \l_my_lipsum_int {6}

% C++:
% l_my_lipsum_int = 6;
%
% Python:
% l_my_lipsum_int = 6

注意观察上面两个命令的参数说明符(冒号后面的字符)，和其后面跟的参数是一一对应的。之后几乎所有的命令都会带有参数说明符，习惯就好，这是L3函数的标准形式。

输出\l_my_lipsum_int乘以142857的值：

\int_eval:n {\l_my_lipsum_int*142857}

% Output:
% 857142
%
% C++:
% std::cout<<l_my_lipsum_int*142857;
%
% Python:
% print(l_my_lipsum_int*142857,end='')

输出是一个形象的说法，这里所谓的输出就是将其放到输出流，也就是显示在最终生成的pdf文件里面。如果仅仅是要输出一个单独变量的值，可以用\int_use:N。

从上面代码可以看到，TeX的注释使用的是%。那如果要对变量取模(很多语言都是使用%作为取模运算符)怎么办。L3编程接口的目标既然是要提供现代语言特性，那自然少不了丰富的库函数（代码只列举了部分，后面内容皆是如此）：

% 代码并不连续，勿大段粘贴运行，仅供说明库函数
\int_set:Nn \l_my_b_int {
    \int_mod:nn {\l_my_a_int}{11} 
} 
% 将\l_my_a_int对11取模并赋值给\l_my_b_int

\int_min:nn {\l_my_a_int} {\l_my_b_int} % 取最小值
\int_max:nn {\l_my_a_int} {\l_my_b_int} % 取最大值
\int_incr:N \l_my_a_int % 自增1，相当于C++: l_my_a_int++;
\int_decr:N \l_my_a_int % 自减1，相当于C++: l_my_a_int--;

% 整数转字母
\int_to_alph:n {11} % -> k
\int_to_Alph:n {12} % -> L

% 转其它进制
\int_set:Nn \l_my_a_int {30}
\int_to_bin:n {\l_my_a_int} % -> 11110
\int_to_hex:n {\l_my_a_int} % -> 1e
\int_to_Hex:n {30} % -> 1E
\int_to_roman:n {321} % -> cccxxi
\int_to_Roman:n {321} % -> CCCXXI

% 转为整数
\int_from_alph:n {z} % -> 26
\int_from_bin:n {1010101} % -> 85
% ...

% 随机整数
\int_rand:n {6} % 1~6之间的随机数
\int_rand:nn {3}{20} % 3~20之间的随机整数

2.32 浮点数（floating point, fp）

浮点数就是带小数点的数，定义和计算跟整数的用法区别不大。

\fp_new:N \l_my_a_fp % 声明
\fp_set:Nn \l_my_a_fp {3.1415} % 赋值
\fp_eval:n {\l_my_a_fp/2.7182} % -> 1.155728055330734

int_eval:n 仅仅支持+、-、*、/、(、)，但是fp_eval:n比int_eval:n 要强大得多。比如三目运算符

\fp_eval:n {1 + 3 > 4 ? 6 : 9} % -> 9
\fp_eval:n {1 + 4 > 4 ? 6 : 9} % -> 6

还有很多其它的运算符都支持，不在此阐述。还有一个重要的功能，就是在\fp_eval:n参数中可以直接使用数学函数！

\fp_use:N \c_pi_fp % -> 3.141592653589793
% \c_pi_fp是常量Pi，可以看出变量名为\c_开头

\fp_eval:n {exp(\c_pi_fp)}     % -> 23.14069263277926
\fp_eval:n {ln(\c_pi_fp)}      % -> 1.1447298858494
\fp_eval:n {sin(\c_pi_fp/4)}   % -> 0.7071067811865474
\fp_eval:n {acos(\c_pi_fp/10)} % -> 1.251225373487637
\fp_eval:n {tand(\c_pi_fp)}    % -> 0.05488615080800332
\fp_eval:n {sqrt(\c_pi_fp)}    % -> 1.772453850905516

2.33 字符串（String, str）

字符串定义，赋值和显示也跟前两种类型大同小异。

\str_new:N \l_my_good_str % 声明
\str_set:Nn \l_my_good_str {!!@^w@r!} % 赋值
\l_my_good_str % 显示

字符串变量可以直接丢进输出流而无需访问函数，L3也提供了一些操作字符串变量的函数：

\str_put_left:Nn \l_my_good_str {ehe}        % 在字符串左边增加内容
\l_my_good_str % -> ehe!!@^w@r!
\str_put_right:Nn \l_my_good_str {d!d}       % 在字符串右边增加内容
\l_my_good_str % -> ehe!!@^w@r!d!d
\str_replace_once:Nnn \l_my_good_str {^} {~} % 替换字符一次
\l_my_good_str % -> ehe!!@ w@r!d!d
\str_replace_all:Nnn \l_my_good_str {!} {l}  % 替换所有字符
\l_my_good_str % -> ehell@ w@rldld
\str_replace_all:Nnn \l_my_good_str {@} {o}  % 替换所有字符
\l_my_good_str % -> ehello worldld

% 取索引（L3中索引从1开始）
\str_item:Nn \l_my_good_str {2} % -> h  
% 字符串切片
\str_range:Nnn \l_my_good_str {2}{-3} % -> hello world

随机访问和切片也支持负数，是不是有Python那味儿了？

2.34 序列（Sequence, seq）

序列(seq)类似Python中的list或C++中的vector，是一种有序的集合。L3中也提供了其它有序容器的数据类型，比如tl(token list)，clist(Comma separated lists)。但个人推荐使用序列(seq)，因为seq比tl更加灵活比clist更加高效(大多数情况下，而clist与LaTeX2e更加兼容)。

声明seq的方法基本和前面声明变量的方法一致

\seq_new:N \l_my_good_seq

声明一个seq其实就是创建了一个空的序列。也可以使用set创建一个带有初始元素的序列：

\seq_set_split:Nnn \l_my_good_seq { , } { a , b , cd , {ef} , g }

可见\seq_set_split:Nnn有三个参数，分别为：

\seq_set_split:Nnn ⟨变量名⟩ {⟨分隔符⟩} {⟨序列内容⟩}

指定分隔符以分割第三个参数的内容，生成含有多个元素的序列。如何将该序列扔到输出流？根据前面所学，可以猜得到应该是一个叫seq_use:Nn的命令。果不其然，我们可以使用该命令指定分隔符以输出序列：

\seq_use:Nn \l_my_good_seq {~=>~}
% Output:
% a => b => cd => ef => g

还有一个更加高级的输出方式：

\seq_use:Nnnn ⟨seq var⟩ {⟨两个之间的分隔符⟩}
{⟨两个以上的分隔符⟩} {⟨最后两个元素的分隔符⟩}

可以指定更多的参数，大家可自行尝试。还可以使用map函数(类似Python的map)进行输出：

% 对\l_my_good_seq中元素应用\uppercase函数输出
\seq_map_function:NN \l_my_good_seq \uppercase
% Output:
% ABCDEFG

上面的\seq_map_function:NN将seq中每个元素作为参数调用了\uppercase函数。仅仅一个\uppercase怎么能实现阁下那无与伦比绝无仅有举世无双的输出构想，那么你可以自己定义一个函数，什么？还没学？L2函数也可以，原生TeX函数也可以，什么也没学，那么你可以使用内联的map函数：

\seq_map_inline:Nn \l_my_good_seq {
    ~[\uppercase{#1}]~
}
% 注意参数说明符的变化
% Output:
% [A] [B] [CD] [EF] [G]

使用内联函数，序列中的每个元素都会自动地绑定到#1上。若是阁下要想更加个性化地输出，可以等到后面学了循环来实现。

seq可以动态地添加，修改和删除元素：

\seq_put_right:Nn \l_my_good_seq {end}  % 在末尾增加一个 end
\seq_put_left:Nn \l_my_good_seq {start} % 在头部增加一个 end

% 在头部删除一个元素，并将该元素放进token list变量\l_tmpa_tl中
\seq_pop_left:NN \l_my_good_seq {\l_tmpa_tl} 
% 同理，在尾部删除一个元素，并将该元素放进token list变量\l_tmpa_tl中
\seq_pop_left:NN \l_my_good_seq {\l_tmpa_tl} 

% 将第二个元素改为 non-end
\seq_set_item:Nnn \l_my_good_seq {2} {non-end}
% 删除第二个元素，并扔进token list变量\l_tmpa_tl中
\seq_pop_item:NnN \l_my_good_seq {2} {\l_tmpa_tl}

与其它编程语言恰恰相反，在左边增删元素反而更加高效

如何根据下标获取序列元素(随机访问)？库函数有该api吗？那肯定有。但是遇到问题就要去查文档吗？可不可以直接推理出来？一门语言的库函数一般都浩如烟海，总归不能去一个个死记硬背。人类远远强于现阶段基于深度学习的人工智能的方面之一便是认知推理，人类认知推理能力何其强大，只要我们第一次看过一只狗的照片，下次看到一只猫，就能立马得出结论:这是一只二哈……

所以，我们可以先不看文档或教程，而直接推测出一个没接触过的api可能会是什么样。比如我们已经知道声明一个新变量基本是<type>_new:N这种形式。那么我们前面已经学过字符串的随机访问了

% 取索引（L3中索引从1开始）
\str_item:Nn \l_my_good_str {2} % -> h  

那么我们可以推测出seq的随机访问则为：

\seq_set_split:Nnn \l_my_good_seq { , } { a, b, c, d, e, f, g }

\seq_item:Nn \l_my_good_seq {1}  % -> a
\seq_item:Nn \l_my_good_seq {4}  % -> d
\seq_item:Nn \l_my_good_seq {-1} % -> g

于字符串的api相比，只是把命令前面的类型名改了即可。再来一个例子，seq在首末删除一个元素不是保存到了一个tl中吗，看看这tl中有什么

\seq_set_split:Nnn \l_my_good_seq { , } { start,end }

% 删除第一个元素 start ，并保存在\l_tmpa_tl中
\seq_pop_left:NN \l_my_good_seq {\l_tmpa_tl}

现在看看\l_tmpa_tl有什么，有同学会说token list(tl)没学过，不会输出。这不刚学了要举一反三，把seq的api名字里的seq替换成tl就成tl的api了(不一定成功，但能减少繁琐的文档阅读)，下面就把seq的map函数改成tl的map函数：

\tl_map_inline:Nn \l_tmpa_tl {
    ~[\uppercase{#1}]~
}
% Output:
% [S] [T] [A] [R] [T]

成功运行，说明人类认知推理取得了极大的成功！仔细观察输出内容，可以推断出\l_tmpa_tl中有5个元素，而我们只从seq里弹出了一个元素，那是因为seq里的一个元素(start)包含多个token(s, t, a, r, t)。

至此，数据类型部分已经讲完了，因为不是文档，该部分只涉及了常用数据类型，若想要学习更多数据类型及其api，可以查看文档或根据前面提到的模式进行推断没学过的api。

2.35 临时变量（Scratch variables）

L3为大多数变量类型预定义了4个临时变量，无需定义便可以使用它们。它们的名字一般为\⟨scope⟩_tmpa_⟨type⟩/和\⟨scope⟩_tmpb_⟨type⟩，因为作用域分为局部和全局，所以2乘以2等于4个。比如序列（seq）的4个临时变量：

\l_tmpa_seq
\l_tmpb_seq
\g_tmpa_seq
\g_tmpb_seq

这些预定义变量是所有代码共享的，因此，要谨慎使用这些变量，以免写出模块间高度耦合的代码。

2.4 流程控制

仅仅学了数据类型是不够的，要想实现各种花里胡哨的逻辑，最核心的就是流程控制，比如条件语句，循环语句（前提阁下不是更花哨地使用布尔运算优化和递归实现条件判断和循环逻辑）。

2.41 条件判断

条件判断其实就是判断布尔值表达式为真还是为假而执行不同分支。在L3中将布尔表达式转化为布尔值的函数成为断言(乱翻译的)函数(Predicate function)，为了不继续错下去，后面使用Predicates指代该函数。Predicates名字一般以_p结尾。一般数据类型都各自实现了自己的Predicates甚至自己的条件判断函数。但本文仅讲比较灵活的api(不是最高效的方式)—\bool_if:nTF + Predicates。

\bool_if:nTF {⟨boolean expression⟩} {⟨true code⟩} {⟨false code⟩}

布尔表达式⟨boolean expression⟩一般由布尔变量(未讲，一般为真或假)和Predicates组成。根据布尔表达式为真还是假相应地执行⟨true code⟩或⟨false code⟩。下面是一个例子：

\str_set:Nn \l_tmpa_str {LaTeX3}
\bool_if:nTF {
    !\int_compare_p:n {4 <= 3 <= 2} % !(4 <= 3 <= 2) 等于 true
    || \str_if_eq_p:nn {latex2} {\l_tmpa_str} % 不相等 false
}
% 最终布尔表达式的值为true，执行 ⟨true code⟩ ，转为大写
{
    \str_uppercase:f{\l_tmpa_str}
}{
    \str_lowercase:f{\l_tmpa_str}
}

% Output:
% LATEX3

很多高级语言都有switch语句，L3亦是：

\int_case:nnF
{ 2 * 5 }
{
    { 5 } { Small }
    { 4 + 6 } { Medium }
    { -2 * 10 } { Negative }
}
{ No idea! }

% Output:
% Medium

因为(2*5) = 10 = (4+6)，所以输出Medium。若是没有任何一个匹配上，则输出No idea!。这里的输出比较简单，可以在代码块里面写更加复杂的逻辑，且case语句还有其它很多花哨的api，大家可自行去了解。

2.4.2 循环

循环能让计算机不知疲倦地做同一件事情成千上万次。大多数其它编程语言都有for循环和while循环。L3中亦有相似功能的实现。

for循环

L3中有很方便使用的for循环api，类似Python中的for循环：

Python:

for i in range(10):
    do_something(i)

LaTeX3:

\int_step_function:nN {10} {\do_something:n}

有一点注意，在L3中，很多东西默认都是从1开始，包括下标，循环初始值。还有就是，诸位可还记得之前提过的seq_map_function:NN和seq_map_inline:Nn。举一反三，自然可以推测到循环有如下api:

\int_step_inline:nn {10} 
{\par This~is~#1}
​
% Output:
% This is 1
% This is 2
% ...
% This is 10

不过此时的#1是循环变量，而之前的是序列元素。循环也可以设置起始值，步长和终止值：

% \int_step_inline:nnnn {⟨起始值⟩} {⟨步长⟩} {⟨终止值⟩} {⟨code⟩}
​
\int_step_inline:nnnn {10} {2} {20}
{\par This~is~#1}
​
% Output:
% This is 10
% This is 12
% This is 14
% ...
% This is 20

也可以使用一个临时变量作为循环变量：

\int_step_variable:nnNn {0} {9} \l_loop_var {
    \par \l_loop_var
}

% 变体还有：
% \int_step_inline:nNn {⟨终止值⟩} ⟨循环变量⟩ {⟨code⟩}
% \int_step_inline:nnNn {⟨起始值⟩} {⟨步长⟩} {⟨终止值⟩} ⟨循环变量⟩ {⟨code⟩}

这种写法等价于Python的：

for l_loop_var in range(10):
    print(l_loop_var)

while循环

while循环仅仅根据布尔表达式的值而决定是否继续，可以使用while循环实现上述逻辑：

\int_set:Nn \l_tmpa_int {10}
\bool_while_do:nn {\int_compare_p:n {\l_tmpa_int <= 20}}{
    \par This~is~ \int_use:N \l_tmpa_int
    % \int_incr:N \l_tmpa_int
    \int_set:Nn \l_tmpa_int {\l_tmpa_int+2} % 每次循环+2
}

% Output:
% This is 10
% This is 12
% This is 14
% ...
% This is 20

L3中还有do-while循环，很简单，仅仅上述代码循环命令中的do和while交换位置即可。

\bool_do_while:nn {⟨布尔表达式⟩} {⟨code⟩}

L3中甚至还有do-until和until-do及其变种(不同的参数说明符)。但这些都可以通过while-do循环实现，就不过多阐述。

牛刀小试

结合编程来画个彩虹图

\documentclass{l3doc}
\usepackage{tikz} 
\usepackage{subfig}


\begin{document}
\ExplSyntaxOn

\seq_set_split:Nnn \g_my_color_seq {,} {red,cyan,green,brown,orange,purple}
\begin{figure*}
    \centering
    \subfloat[Rotate~$60^\circ$]{
        \begin{tikzpicture}[scale=0.6]
            \fp_step_inline:nnnn {1}{1}{360}{
                \draw [\seq_item:Nn \g_my_color_seq {\int_mod:nn{#1}{6}+1}] 
                      (\int_mod:nn{#1-1}{6}*60+#1 \c_colon_str \fp_eval:n{(#1-1)/60}) -- 
                      (\int_mod:nn{#1}{6}*60+#1 \c_colon_str #1/60);
            }
        \end{tikzpicture}
    }
    \subfloat[Rotate~$30^\circ$]{
        \begin{tikzpicture}[scale=0.6]
            \fp_step_variable:nnnNn {1}{1}{360}{\i}{
                \draw [
                    \int_case:nn {\int_mod:nn{\i}{6}}
                    {
                        {0} {magenta}
                        {1} {lime}
                        {2} {olive}
                        {3} {orange}
                        {4} {pink}
                        {5} {violet}
                    } 
                ] 
                      (\int_mod:nn{\i-1}{6}*30+\i \c_colon_str \fp_eval:n{(\i-1)/60}) -- 
                      (\int_mod:nn{\i}{6}*30+\i \c_colon_str \i/60);
            }
        \end{tikzpicture}
    }
\end{figure*}
\ExplSyntaxOff
\end{document}

该代码涵盖了条件判断，循环等等知识。值得注意的是，tikz画图中用的是极坐标，极坐标的表示需要冒号，而冒号在L3环境中被转义了，所以采用\c_colon_str代替冒号。最终得到的pdf长这样：

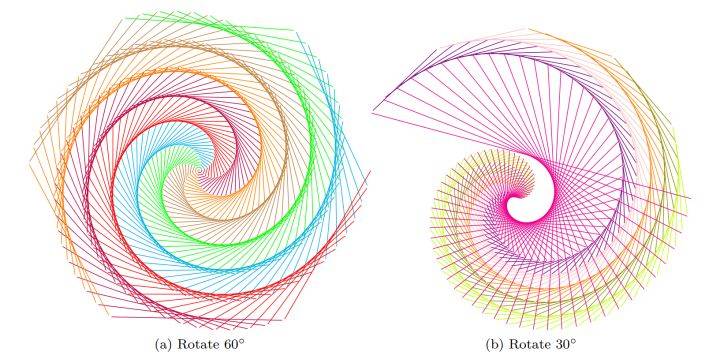
2.5 函数

在L3中，定义函数其实就是定义命令，对函数操作的api基本都以cs_开头。在2.2节推测过，定义函数的命令具有如下形式：

的确如此，定义一个L3函数最标准的形式便是：

\cs_new:Npn ⟨函数名⟩ ⟨参数⟩ {⟨code⟩}

比如定义一个计算两个数之和的函数\my_add:nn：

\cs_new:Npn \my_add:nn #1#2 {
    #1 + #2
}

在L3中参数的声明基本和L2一致，都是#打头加数字，但最多使用9个参数，具体详见\newcommand实现原理。调用并输出\my_add:nn：

\int_eval:n {
    \my_add:nn {123} {456}
} 
% Output:
% 579

函数和变量不同，无需提前声明也能赋值。所以也可以使用\cs_set:Npn创建函数：

\cs_set:Npn ⟨函数名⟩ ⟨参数⟩ {⟨code⟩}

但后者不会去判断是否已经定义，因此使用\cs_set:Npn可能会覆盖原函数。

函数带有了参数说明符之后，编译器能够自动推导参数个数，因此#1#2这种文本可以省略，如下代码：

\cs_new:Nn \my_add:nn {
    #1 + #2
}

注意参数说明符的变化，省略掉了#1#2同时，\cs_new的参数说明符也从Npn变成了Nn。

2.6 宏展开控制

前面两种方法仅仅允许定义基本函数（base function），基本函数只能使用之前2.2节中介绍过的几个参数说明符N,n,T,F,p,w。而仅仅使用这些参数说明符并不能很好地进行宏展开控制。下面增加几个参数的说明：

c： 会将接收的值转为命令，即\foo:c {cmd}等价于\foo:N \cmd

V & v： 接收命令的值，V类似N接收一个命令，而v类似于c

x & f&o： 接收参数展开后的内容，x接收参数进行完全展开后的内容，f接收参数展开到第一个不能展开的token为止，而o接收对参数展开一次后的内容

\cs_generate_variant:Nn

使用命令\cs_generate_variant:Nn能够修改一个函数的参数说明符，产生一个函数的变种（variant），可以为基本函数定义个性化的参数描述符。其使用方式如下：

\cs_generate_variant:Nn ⟨要修改的函数⟩ {⟨新的参数说明符⟩}

下面是一个例子：

\def\ver{3}
\str_new:N \my_version
\cs_new:Nn \my_set_version:nn {
    \str_set:Nn \my_version {#1~#2} 
}
\my_set_version:nn {LaTeX} {\ver}
\par \my_version % -> LaTeX \ver

希望第4行\my_version的输出应该是LaTeX 3，然而实际输出却是LaTeX \ver。因此需要使用\cs_generate_variant:Nn来定义能够处理这种情况的变种函数。

% 将\my_set_version的参数说明符由nn改为nV
\cs_generate_variant:Nn \my_set_version:nn {nV}
​
\my_set_version:nV {LaTeX} {\ver}
\par \my_version % -> LaTeX 3

生成一个\my_set_version:nn的变种函数\my_set_version:nV，如此，该函数接收的第二个参数为\ver的值而非它本身。

使用\cs_generate_variant:Nn可以很灵活的生成函数的变种以控制宏展开，甚至还可以修改L3内部函数的参数描述符定义。但其也有一些限制：

• N改为c
• n改为o，V，v，f，x，e

\exp_args

每适配一种情况就声明一个新函数变种何其繁琐。\exp_args也能够以一种更加简单的方式，且无须定义新函数变种来控制函数的参数说明符。上述例子用\exp_args命令一行便能解决：

\exp_args:NnV \my_set_version:nn {LaTeX} {\ver}
\par \my_version % -> LaTeX 3

其用法也很简单，只需要在其冒号后按自己需要的方式进行填写参数说明符即可，如下：

\exp_args的第一个参数描述符为N，表示接收要暂时修改的函数，自第二个开始便依次对应函数的参数该如何展开。而且可以在合适位置停止而只控制部分参数，即如下这种情况也是可以的。

\exp_args:NV \my_set_version:nn {\ver} {other contents}

假若有一个嵌套的clist：

\clist_set:Nn \l_tmpa_clist {1,2,3,4}
\clist_set:Nn \l_tmpb_clist {\l_tmpa_clist}

现在需要通过外层list输出内层list的值，根据前面所学可以写为：

% ****输出****|-----------取第一个元素-----------|*分隔符*
\clist_use:Nn \clist_item:Nn \l_tmpb_clist {1}   {|}

但\clist_use:Nn第一个参数是接收一个命令，此时这样写显然是错误的。因此需要对[取第一个元素]的内容提取展开。因此，可以使用\exp_args控制\clist_use:Nn第一个参数的展开：

\exp_args:Nx \clist_use:Nn {\clist_item:Nn \l_tmpb_clist {1}} {|}

最终输出正确的结果：

2.7 函数牛刀小试

使用函数可以简化代码的编写，将一些会重复使用的代码块封装成函数，避免代码冗余。LaTeX3中的函数也可以调用自身，实现递归。比如经典的汉诺塔问题，便可会议通过函数的递归轻松实现：

\cs_new:Nn \my_hanoi:nnnn {
    \bool_if:nTF {\int_compare_p:n {#1=0}}{}
    {
        \my_hanoi:nnnn {\int_eval:n {#1-1}} {#2} {#4} {#3}
        \par Move~#1~from~#2~to~#3~through~#4
        \my_hanoi:nnnn {\int_eval:n {#1-1}} {#4} {#3} {#2}
    }
}

调用该函数：

\my_hanoi:nnnn {3} {A} {B} {C}

输出的内容为三个盘时汉诺塔问题的解决办法：

Move 1 from A to B through C
Move 2 from A to C through B
Move 1 from B to C through A
Move 3 from A to B through C
Move 1 from C to A through B
Move 2 from C to B through A
Move 1 from A to B through C

有点单调，不够直观，不够花哨。可以使用beamer和tikz自动生成ppt动画。具体代码后面整理后会公布（代码详见latex3-hanoi），结果长这样：

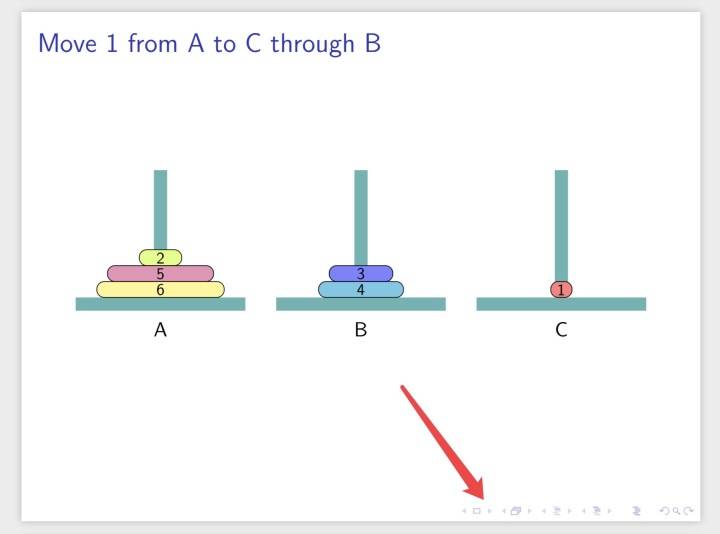
点击下一页会出现下一个状态：

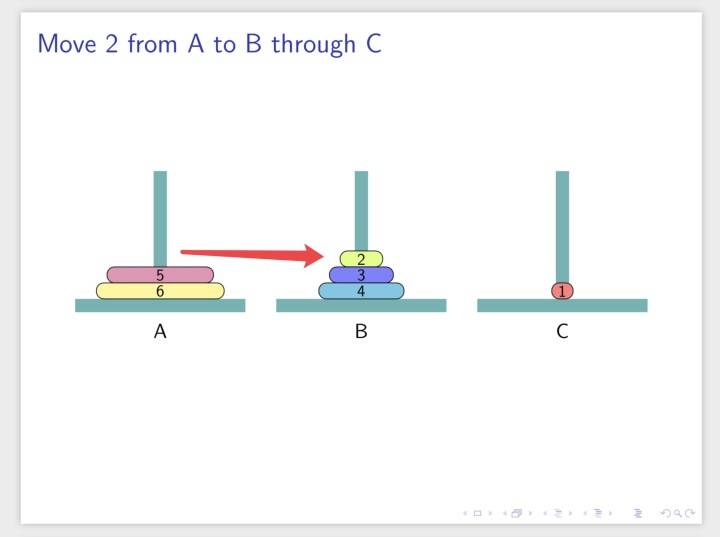
播放幻灯片效果为：

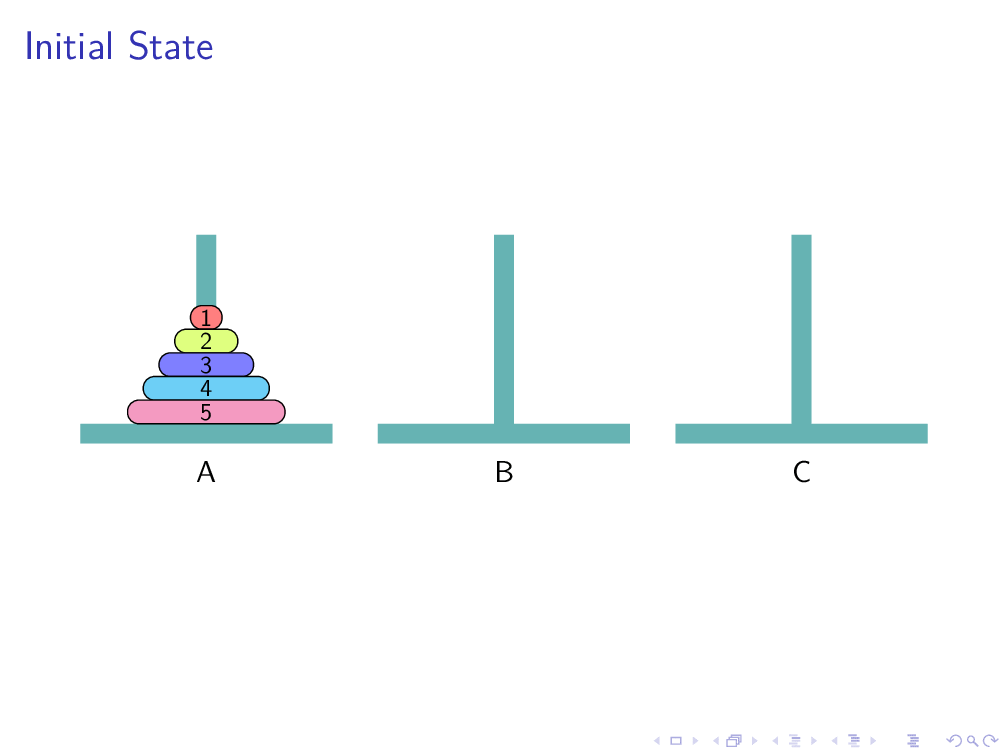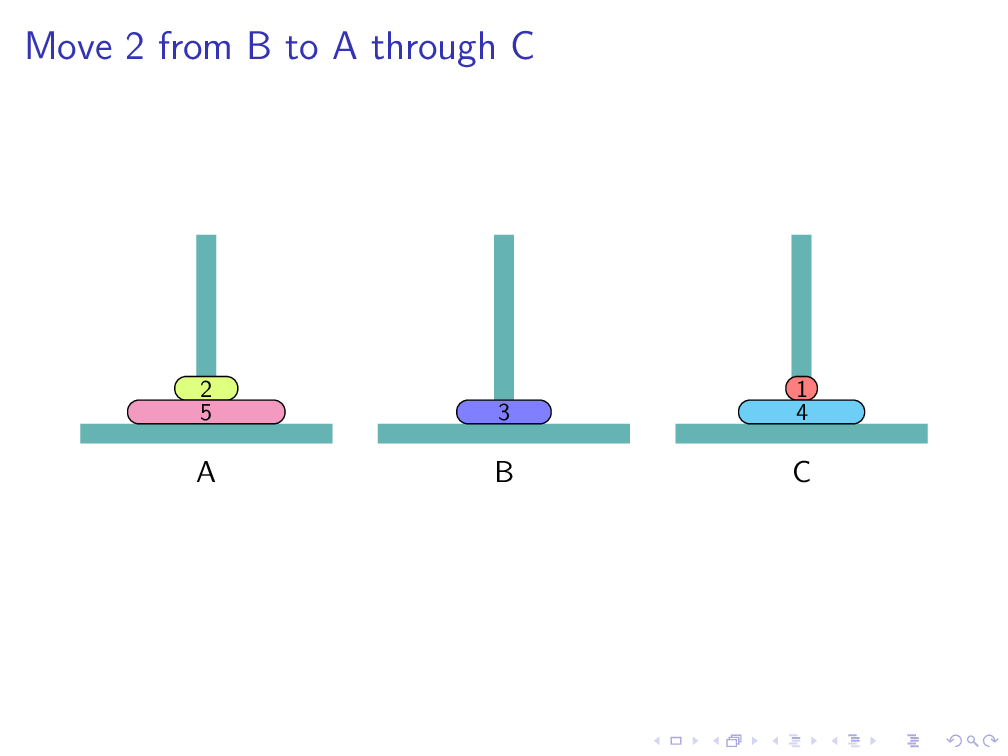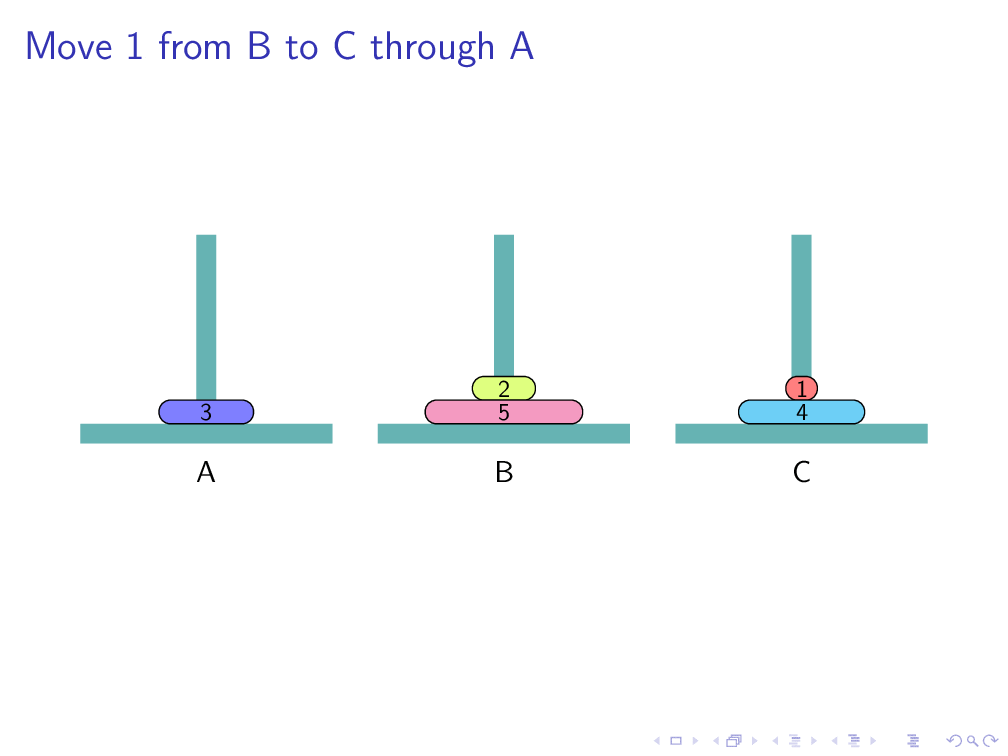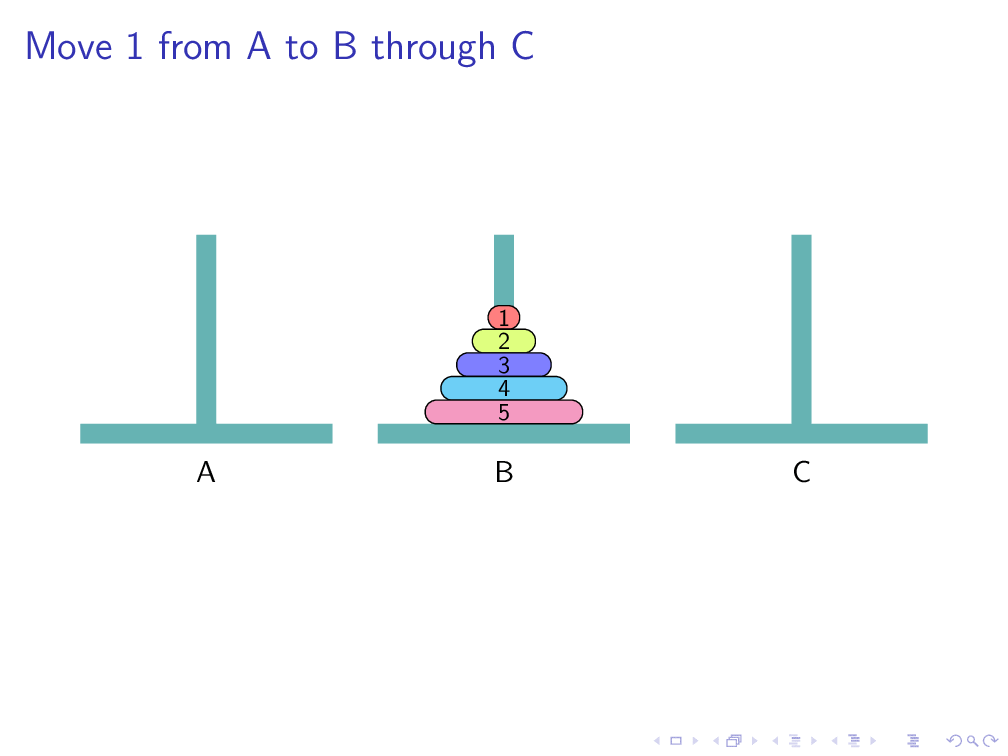
3 结束语

自此，该文章已经结束。

本来该文章的标题我是想取一份简洁的LaTeX3教程。

内容应该涵盖：

• 数据类型
• 流程控制
• 函数及宏展开控制
• 正则表达式
• 文件IO
• …

然而在写作过程中却发现控制不住篇幅，发现该文章已经有点不简洁了！（Typora的计数两万字符左右）。最终缩减为：

• 数据类型
• 流程控制
• 函数及宏展开控制

个人不喜欢一个很长很长的文章，读者看起来也难受。剩下的其它内容则考虑在本专栏另建文章展开了。

本文章也未必是结束了，后续可能会根据情况和大家反馈对文章进行追更修改。文中难免会有疏漏和个人理解有出入的地方，还请各位读者在评论区指出，然后我会及时修改。

4 参考资料

expl3.pdf

interface3.pdf

source3.pdf

l3styleguide.pdf