100 如何使用l3coffin找到合适的锚点拼接以实现嵌套积分号排版
发布于 2024-09-19 21:39:43
林间花老师指出如下的嵌套积分是简单的😊
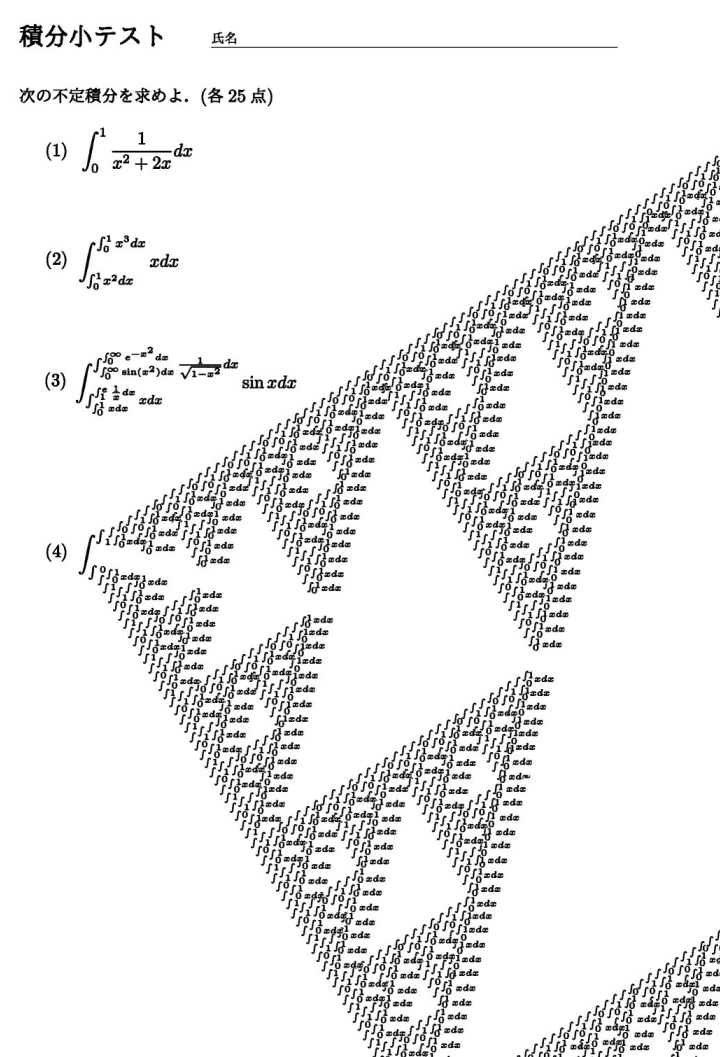
在尝试学习了l3coffin后实现已经实现了从对于coffin中的积分号,先后在其右上和右下位置处添加新的coffin连接的"轮子",如下面的代码:
\documentclass{article}
\usepackage[margin=2cm,a2paper]{geometry}
\usepackage{amsmath}
\usepackage{xcolor}
\usepackage{xcoffins}
\usepackage{graphicx}
\newcommand{\diffx}{$\mathrm{d}x$}
\newcommand{\myint}[1][8]{\scalebox{#1}{$\int$}}
\newcommand{\numzero}[1][8]{\scalebox{#1}{$0$}}
\newcommand{\numone}[1][8]{\scalebox{#1}{$1$}}
\begin{document}
\ExplSyntaxOn
%改进\coffin_reset_poles:N的c功能并将其封装为\my_coffin_reset:n
\cs_generate_variant:Nn \coffin_reset_poles:N {c}
\cs_new:Nn \my_coffin_reset:n % <coffin>
{
\coffin_reset_poles:c {l_tmp#1_coffin}
}
\cs_set_nopar:Nn \newSetCof:nn {
%重新封装coffins命令,若不存在,则新建名为l_tmp#1_coffin的新coffin
%之后设置hcoffin的matrial内容为#2
\coffin_if_exist:cF {l_tmp#1_coffin}
{\coffin_new:c {l_tmp#1_coffin}}
\hcoffin_set:cn {l_tmp#1_coffin}{#2}
}
\cs_set_nopar:Nn \useCof:n {
%控制输出coffin,默认按照手柄位置handles{l,b}进行对齐
%\coffin_typeset:cnnnn {l_tmp#1_coffin} {l} {b} {0pt} {0pt}
\coffin_display_handles:cn {l_tmp#1_coffin} {magenta}
}
\cs_set_nopar:Nn \setIntPolesUpper:n {%设置上半对齐点位
\my_coffin_reset:n {#1}
\coffin_set_horizontal_pole:cnn {l_tmp#1_coffin}{upperh}{0.95 \coffin_ht:c {l_tmp#1_coffin}}% 0.8 height pole set
\coffin_set_vertical_pole:cnn {l_tmp#1_coffin}{upperv}{0.88 \coffin_wd:c {l_tmp#1_coffin}}
% then we can use the handle (upperv,upperh) for the upper one
}
\cs_set_nopar:Nn \setIntPolesLower:n {
\my_coffin_reset:n {#1}%设置下半对齐点位
\coffin_set_horizontal_pole:cnn {l_tmp#1_coffin}{lowerh}{-0.3 \coffin_ht:c {l_tmp#1_coffin}}% -0.25 height pole set
% \coffin_set_vertical_pole:Nnn {\l_tmpI_coffin}{baselow}{0pt}
\coffin_set_vertical_pole:cnn {l_tmp#1_coffin}{lowerv}{0.85 \coffin_wd:c {l_tmp#1_coffin}}
% then we can use the handle (lowerv,lowerh) for the upper one
}
%关键的核心封装命令\intgral_coffin_join:nnn <intgral-within-coffin> <content1> <content2>
\cs_new:Nn \intgral_coffin_join:nnn {
% #1=base #2 = \myint[4] #3 = \numone[4]
%处理流程:
%(1) reset coffin poles with base
\my_coffin_reset:n {#1}
%(2) new_coffin_with_tmpA with matrial #2
\newSetCof:nn {A} {#2}
%(3) join base with upper_part tmpA with handles (upperv,upperh) (l,vc)
\setIntPolesUpper:n {#1}
\coffin_join:cnncnnnn {l_tmp#1_coffin} {upperv} {upperh} {l_tmpA_coffin} {l} {vc} {0pt} {0pt}
%(4) reset coffin poles with base
\my_coffin_reset:n {#1}
% %(5) new_coffin_with_tmpB with matrial #3
\newSetCof:nn {B} {#3}
% %(6) join base with lower_part tmpB with handles (lowerv,lowerh) (l,vc)
\setIntPolesLower:n {#1}
\coffin_join:cnncnnnn {l_tmp#1_coffin} {lowerv} {lowerh} {l_tmpB_coffin} {l} {vc} {0pt} {0pt}
%(7) reset coffin poles with base
\my_coffin_reset:n {#1}
% return => joined and poles-reset coffin "base"
}
\newSetCof:nn {base}{\myint}
\my_coffin_reset:n {base}
\useCof:n {base}
% test for command \intgral_coffin_join
% \intgral_coffin_join:nnn {base}{\myint[4]}{\numone[4]}
% \useCof:n {base}
\int_step_inline:nn {6}{
\intgral_coffin_join:nnn {base}{\myint[5]}{\myint[5]}
\useCof:n {base} \par
}
\ExplSyntaxOff
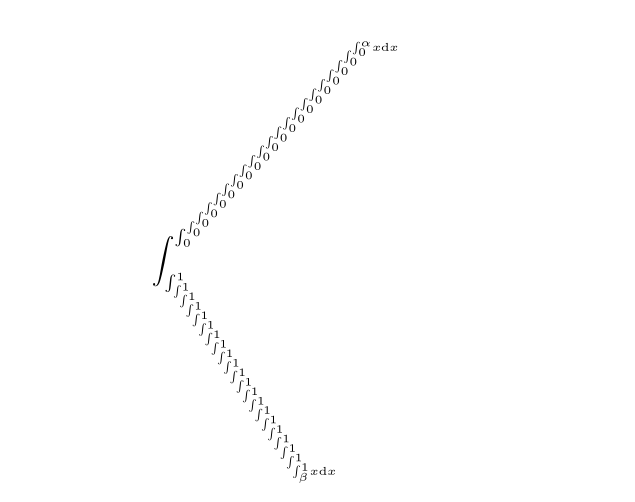
\end{document}其中关键代码已做注释,\intgral_coffin_join:nnn用于实现一次coffin的拼接,实现的效果如下: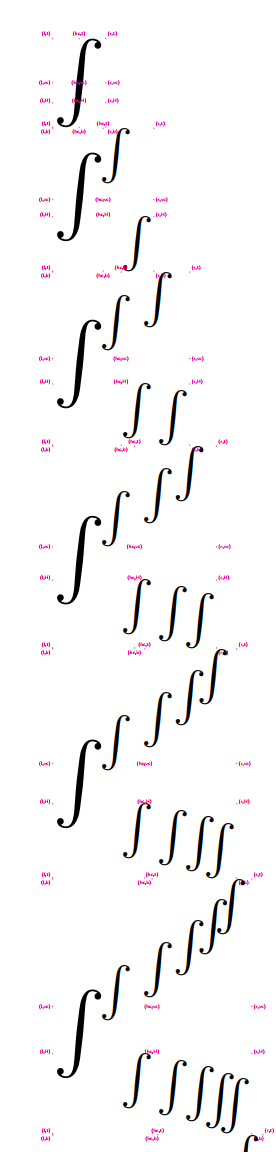
现阶段存在的问题是:
- 在默认的积分号的倾斜角度下,是否容易找到合适的定位「superscript」和「subscript pattern」(例如使用的水平或者垂直
pole进行定位的距离符合某一等比数列),或者改用垂直积分号 - 使用递归等方式找到原图的重复规律(这种规律不一定是真实存在的,原图的转发者透露该图是使用类似
photoshop等软件制作的)只要能实现这种类似"分形"的效果就可以...
有关可汇总和参考的代码如下压缩包文件nested-integral.zip
(Un)Happy TeXing!
Edited: 2025-12-04
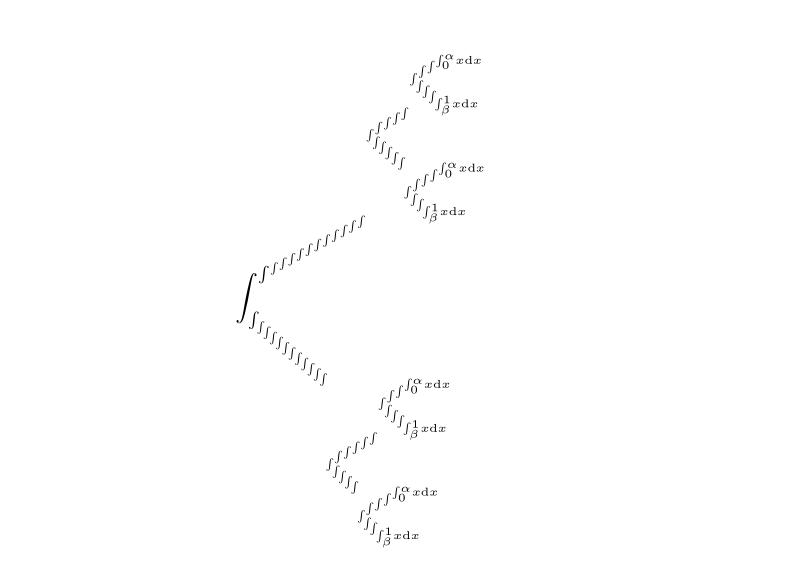
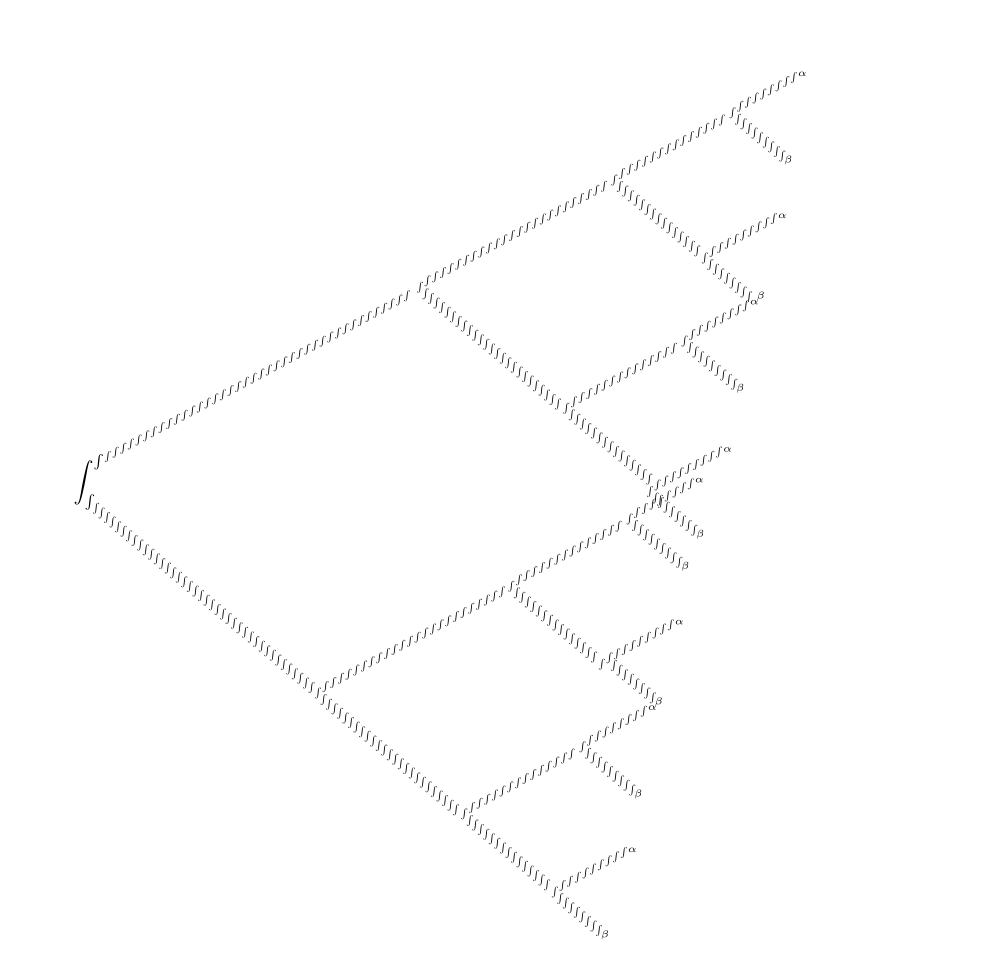
林间花老师又补充了一个图
来自:

其递推结构为...

现在问题的关键主要是找到原问题的递归结构....
关注者
0
被浏览
1.7k










差评,不贴
\raisemath的来源😡