如何调节align环境中公式的上下间距?
发布于 2021-09-25 15:30:14
\begin{align*}
\mb{u}'=\frac{\mr{d}\mb{r}'}{\mr{d}t'}&=(\frac{\mr{d}x'}{\dd t'},\frac{\mr{d}y'}{\dd t'},\frac{\mr{d}z'}{\dd t'})\\[10bp]
&=(\frac{-\dfrac{v}{\sqrt{1-\beta^2}}\dd t+\dfrac{1}{\sqrt{1-\beta^2}}\dd x}{\dfrac{1}{\sqrt{1-\beta^2}}\dd t-\dfrac{\dfrac{v}{c^2}}{\sqrt{1-\beta^2}}\dd x},\frac{\mr{d}y}{\dfrac{1}{\sqrt{1-\beta^2}}\dd t-\dfrac{\dfrac{v}{c^2}}{\sqrt{1-\beta^2}}\dd x},\frac{\mr{d}z}{\dfrac{1}{\sqrt{1-\beta^2}}\dd t-\dfrac{\dfrac{v}{c^2}}{\sqrt{1-\beta^2}}\dd x})\\[10bp]
&=(\dfrac{u_x-v}{1-\dfrac{vu_x}{c^2}},\dfrac{\sqrt{1-\beta^2}u_y}{1-\dfrac{vu_x}{c^2}},\dfrac{\sqrt{1-\beta^2}u_z}{1-\dfrac{vu_x}{c^2}})
\end{align*}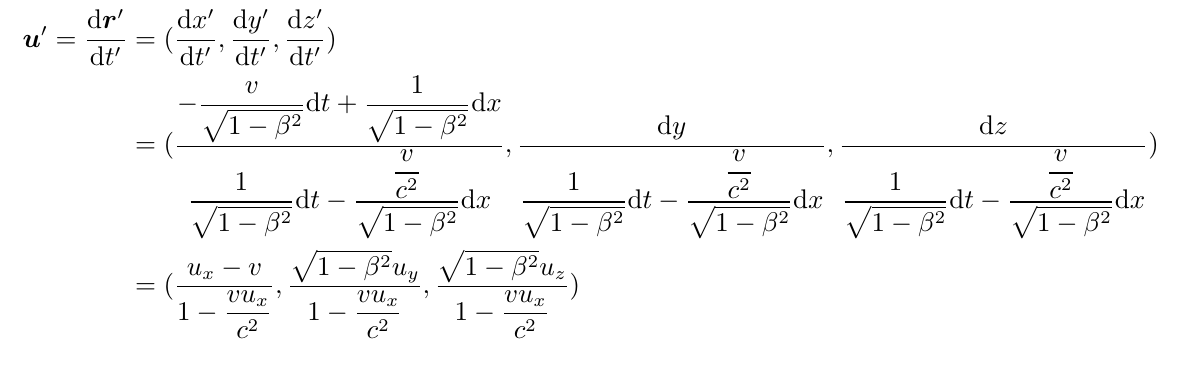
关注者
0
被浏览
7.2k






这里面有些我自定义的命令